Generer Pascals trekant i Python: 3 enkle metoder

0 Shares

Denne veiledningen vil introdusere deg til prosessen med å generere Pascals trekant i Python for et spesifikt antall rader.

Vi begynner med å undersøke hvordan Pascals trekant er bygget opp. Deretter vil vi utvikle en Python-funksjon for å realisere dette, og utforske metoder for å forbedre effektiviteten.

▶️ La oss sette i gang!

Hva er Pascals trekant, og hvordan konstrueres den?

Å generere Pascals trekant for et gitt antall rader er en populær oppgave i intervjuer for programmerere.

I Pascals trekant, med «n» antall rader, vil rad nummer «i» inneholde «i» antall elementer.

Følgelig består den første raden av et enkelt element, som er 1. Hvert påfølgende element på de neste radene er summen av de to tallene som står direkte over det.

Illustrasjonen nedenfor viser hvordan Pascals trekant konstrueres for fem rader.

Pascals trekant for numRows = 5 (Illustrasjon av forfatteren)

Det er viktig å merke seg at når det kun er et enkelt tall over et element, fylles tomrommet med nuller.

📝Som en rask øvelse, prøv selv å konstruere Pascals trekant for «n = 6» og «n = 7» ved å følge den samme metoden.

Nå skal vi begynne å skrive kode. Du kan velge å utføre kodeeksemplene i en nettleserbasert Python IDE, som tipsbilk.net tilbyr, mens du følger denne veiledningen.

Python-funksjon for å generere Pascals trekant

I dette avsnittet skal vi skape en Python-funksjon som genererer Pascals trekant basert på det angitte antall rader.

Det er to nøkkelspørsmål som må adresseres:

Hvordan representerer vi tallene i Pascals trekant?
Hvordan utformer vi utskriften av Pascals trekant med riktig mellomrom og formatering?

La oss gå igjennom disse nå.

#1. Hvordan uttrykker vi hvert element i Pascals trekant?

Det viser seg at elementene i Pascals trekant kan finnes ved hjelp av formelen for «nCr». Fra matematikken du lærte på skolen, husker du kanskje at «nCr» viser til antall måter du kan velge «r» elementer fra et sett på «n» elementer.

Formelen for «nCr» er vist nedenfor:

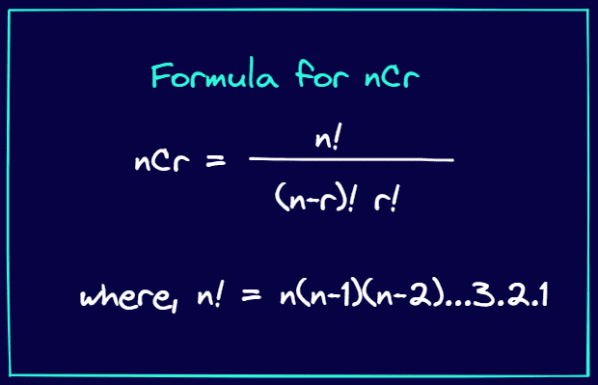nCr formel (Illustrasjon av forfatteren)

La oss bruke nCr-formelen til å uttrykke elementene i Pascals trekant.

Pascals trekantelementer ved hjelp av nCr (Illustrasjon av forfatteren)

Vi har nå identifisert en metode for å uttrykke elementene i matrisen.

#2. Hvordan håndterer vi avstanden når vi skriver ut mønsteret?

I Pascals trekant med «numRows» vil rad nummer 1 ha et element, rad nummer 2 vil ha to elementer, og så videre. For å generere trekantformen, behøves «numRows – i» mellomrom på rad nummer «i». Vi kan bruke Pythons «range»-funksjon sammen med en «for»-løkke for å oppnå dette.

Siden «range»-funksjonen ekskluderer endepunktet som standard, må vi legge til «+ 1» for å oppnå det nødvendige antall innledende mellomrom.

Nå som du har forstått hvordan elementene kan representeres, og hvordan vi skal håndtere mellomrom, kan vi fortsette med å definere funksjonen «pascal_tri».

Analyse av funksjonsdefinisjonen

Hva skal funksjonen «pascal_tri» gjøre?

Funksjonen «pascal_tri» skal ta antall rader («numRows») som argument.
Den skal skrive ut Pascals trekant med det spesifiserte antall rader.

For å beregne fakultetet, kan vi bruke «factorial»-funksjonen fra Pythons innebygde «math»-modul.

▶️ Kjør følgende kode for å importere «factorial» og bruke den i den nåværende modulen.

from math import factorial

Kodeutdraget nedenfor inneholder funksjonsdefinisjonen.

def pascal_tri(numRows):
  '''Genererer Pascals trekant med numRows.'''
  for i in range(numRows):
    # Løkke for å generere ledende mellomrom
	  for j in range(numRows-i+1):
		  print(end=" ")
    
    # Løkke for å generere elementer på rad i
	  for j in range(i+1):
		  # nCr = n!/((n-r)!*r!)
		  print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")

	 # Skriv ut hver rad på en ny linje
	  print("\n")

Funksjonen fungerer på følgende måte:

Funksjonen «pascal_tri» har en påkrevd parameter, «numRows», som representerer antall rader.
Det vil totalt være «numRows» rader. For hver rad «i» legger vi til «numRows – i» antall ledende mellomrom før det første elementet på raden.
Deretter bruker vi nCr-formelen for å kalkulere de individuelle elementene. For rad «i» er elementene «iCj», hvor j = {0,1,2,..,i}.
Legg merke til at vi bruker heltallsdivisjon «//», da vi ønsker heltall som elementer.
Etter å ha kalkulert alle elementene på en rad, skriver vi ut neste rad på en ny linje.

🔗 Siden vi har lagt til en docstring, kan du bruke Pythons innebygde «help»-funksjon eller «__doc__»-attributtet for å hente funksjonens docstring. Kodeeksemplet nedenfor viser hvordan du gjør dette.

help(pascal_tri)

# Output
Help on function pascal_tri in module __main__:

pascal_tri(numRows)
    Genererer Pascals trekant med numRows.

pascal_tri.__doc__

# Output
Genererer Pascals trekant med numRows.

La oss nå fortsette og kalle funksjonen med antall rader som argument.

pascal_tri(3)

# Output
     1
    1 1
   1 2 1

De tre første radene i Pascals trekant skrives ut som forventet.

Generere Pascals trekant ved hjelp av rekursjon

I forrige avsnitt identifiserte vi det matematiske uttrykket for hvert element i Pascals trekant. Vi brukte imidlertid ikke forholdet mellom elementene på to påfølgende rader.

Faktisk brukte vi den forrige raden for å kalkulere elementene i neste rad. Kan vi ikke dra nytte av dette for å lage en rekursiv implementering av funksjonen «pascal_tri»?

Ja, la oss gjøre det!

I en rekursiv implementering kaller en funksjon seg selv gjentatte ganger, til et grunntilfelle er nådd. I konstruksjonen av Pascals trekant starter vi med den første raden med elementet 1, og bygger deretter de påfølgende radene.

Funksjonskallet «pascal_tri(antallRader)» vil igjen kalle «pascal_tri(antallRader-1)» og så videre, helt til grunntilfellet «pascal_tri(1)» er nådd.

Se for deg eksempelet der du skal skrive ut de tre første radene i Pascals trekant. Illustrasjonen nedenfor viser hvordan de rekursive kallene blir plassert på stakken, og hvordan de rekursive funksjonskallene returnerer radene i Pascals trekant.

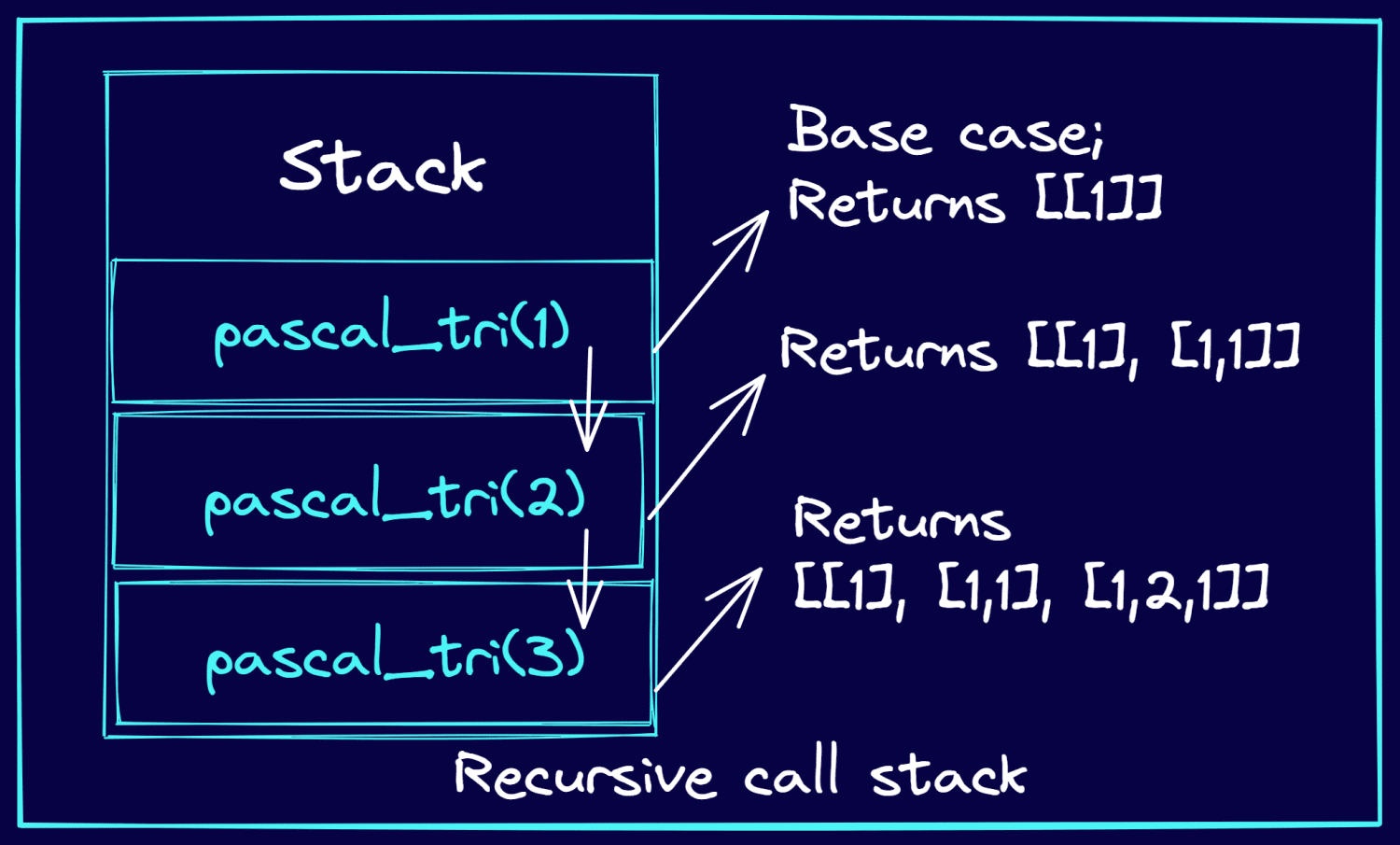Anropsstabel under rekursive kall (Illustrasjon av forfatteren)

▶️ Kjør kodeeksemplet nedenfor for å generere radene i Pascals trekant rekursivt.

def pascal_tri(numRows):
    '''Genererer Pascals trekant med numRows.'''
    if numRows == 1:
        return [[1]] # Grunntilfelle er nådd!
    else:
        res_arr = pascal_tri(numRows-1) # Rekursivt kall til pascal_tri
        # Bruk forrige rad til å beregne nåværende rad
        cur_row = [1] # Hver rad begynner med 1
        prev_row = res_arr[-1]
        for i in range(len(prev_row)-1):
            # Sum av de 2 elementene rett over
            cur_row.append(prev_row[i] + prev_row[i+1])
        cur_row += [1] # Hver rad slutter med 1
        res_arr.append(cur_row)
        return res_arr

Her er noen viktige punkter å merke seg:

Vi har brukt en nestet liste som datastruktur, der hver rad i Pascals trekant er en liste i seg selv: [[rad 1], [rad 2],…,[rad n]].
Funksjonskallet «pascal_tri(numRows)» utløser en serie rekursive kall med argumentene «numRows – 1», «numRows – 2» helt ned til 1. Disse kallene plasseres på en stakk.
Når «numRows == 1» har vi nådd grunntilfellet og funksjonen returnerer [[1]].
Den returnerte listen benyttes deretter av de påfølgende funksjonene i anropsstakken for å beregne neste rad.
Hvis «cur_row» er den aktuelle raden, vil «cur_row[i]» være lik «forrige_rad[i] + prev_row[i+1]» – altså summen av de to elementene rett over gjeldende indeks.

Siden den returnerte matrisen er en nestet liste (liste av lister), må vi justere mellomrom og skrive ut elementene, som vist i kodeeksemplet nedenfor.

tri_array = pascal_tri(5)

for i,row in enumerate(tri_array):
  for j in range(len(tri_array) - i + 1):
    print(end=" ") # Ledende mellomrom
  for j in row:
    print(j, end=" ") # Skriv ut elementer
  print("\n")  # Skriv ut ny linje

Utdataene er korrekte, som vist nedenfor!

Python-funksjon for å generere Pascals trekant for antall rader ≤ 5

Begge metodene vi har gått gjennom fungerer for å generere Pascals trekant for et vilkårlig antall rader («numRows»).

Det finnes imidlertid situasjoner der du kun har behov for Pascals trekant med et lite antall rader. Når antallet rader du skal generere er 5 eller mindre, kan du bruke en enklere teknikk.

Se figuren nedenfor og observer hvordan potensen av 11 korresponderer med elementene i Pascals trekant. Det er viktig å merke seg at dette kun fungerer opp til den 4. potensen av 11. Det vil si at 11 opphøyd i potens {0, 1, 2, 3, 4} gir elementene i rad 1 til 5 i Pascals trekant.

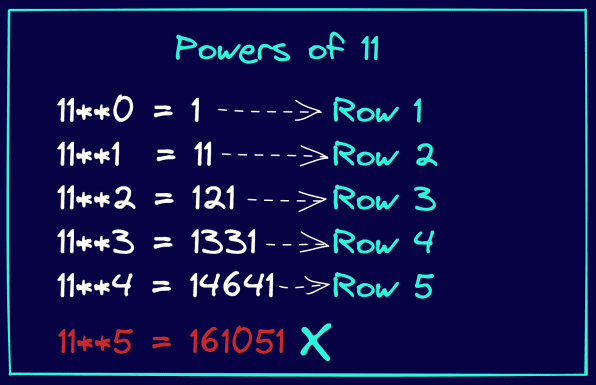
La oss definere funksjonen på nytt, som vist nedenfor:

def pascal_tri(numRows):
  '''Genererer Pascals trekant med numRows.'''
  for i in range(numRows):
    print(' '*(numRows-i), end='')
    # Beregn potensen av 11
    print(' '.join(str(11**i)))

Slik fungerer «pascal_tri»-funksjonen:

Som i de tidligere eksemplene justerer vi mellomrommet.
Vi bruker Pythons eksponentieringsoperator (**) for å beregne potensen av 11.
Siden potensen av 11 er heltall som standard, konverterer vi dem til en streng ved å bruke «str()». Nå har du potensen av 11 som strenger.
Strenger i Python er iterable, noe som betyr at du kan iterere gjennom dem og få tilgang til ett tegn om gangen.
Deretter kan du bruke «join()»-metoden med syntaksen: <sep>.join(<iterable>) for å kombinere elementene i <iterable> ved hjelp av <sep> som skilletegn.
Her trenger vi et enkelt mellomrom mellom tegnene, så <sep> blir « «, og <iterable> er strengen: potensen av 11.

La oss se om funksjonen fungerer som den skal.

pascal_tri(5)

# Output
     1
    1 1
   1 2 1
  1 3 3 1
 1 4 6 4 1

Som et annet eksempel, kall funksjonen «pascal_tri» med 4 som argument.

pascal_tri(4)

# Output
     1
    1 1
   1 2 1
  1 3 3 1

Forhåpentligvis har du nå en god forståelse for hvordan du enkelt kan generere Pascals trekant med antall rader i området 1 til 5.

Konklusjon

Dette er hva vi har lært:

Hvordan konstruere Pascals trekant med et spesifisert antall rader. Hvert tall på hver rad er summen av de to tallene rett over.
Utvikle en Python-funksjon som bruker formelen «nCr = n!/(n-r)!.r!» for å beregne elementene i Pascals trekant.
Vi har lært om en rekursiv implementering av funksjonen.
Til slutt lærte vi den mest optimale metoden for å generere Pascals trekant for et antall rader opp til 5 – ved hjelp av potensen av 11.

Hvis du ønsker å utvikle Python-ferdighetene dine videre, kan du lære hvordan du multipliserer matriser, sjekker om et tall er primtall eller løser strenghåndteringsproblemer. Lykke til med kodingen!