Oppdag alt du trenger å vite om utforskende dataanalyse, en avgjørende prosess for å identifisere tendenser og mønstre, samt oppsummere datasett ved bruk av statistiske sammendrag og grafiske fremstillinger.
Som med alle prosjekter, er et datavitenskapelig prosjekt en omfattende prosess som krever tid, god organisering og nøyaktig oppfølging av flere faser. Utforskende dataanalyse (EDA) er en av de mest sentrale trinnene i denne prosessen.
I denne artikkelen skal vi derfor se nærmere på hva utforskende dataanalyse er og hvordan du kan bruke det med R!
Hva innebærer utforskende dataanalyse?
Utforskende dataanalyse innebærer undersøkelse og kartlegging av egenskapene til et datasett før det anvendes i en konkret applikasjon, enten det er forretningsmessig, statistisk eller innen maskinlæring.
Denne sammenfatningen av informasjonsinnholdet og de viktigste karakteristikkene utføres ofte ved hjelp av visuelle metoder, som grafer og tabeller. Denne praksisen gjennomføres i forkant for å vurdere potensialet i dataene, som senere vil gjennomgå en mer avansert behandling.
EDA muliggjør derfor:
- Formulering av hypoteser for bruken av den aktuelle informasjonen;
- Avdekking av skjulte detaljer i datastrukturen;
- Identifisering av manglende verdier, avvikende verdier eller uvanlig oppførsel;
- Oppdagelse av overordnede trender og relevante variabler;
- Fjerning av irrelevante variabler eller variabler som korrelerer med andre;
- Bestemmelse av den formelle modelleringen som skal benyttes.
Hva skiller beskrivende og utforskende dataanalyse?
Det eksisterer to hovedtyper av dataanalyse: beskrivende analyse og utforskende dataanalyse. Disse går ofte hånd i hånd, til tross for at de har ulike mål.
Mens den beskrivende analysen konsentrerer seg om å beskrive oppførselen til variabler, som gjennomsnitt, median, modus osv.,
tar den utforskende analysen sikte på å identifisere relasjoner mellom variabler, utlede foreløpige innsikter og styre modelleringen mot de vanligste maskinlæringsparadigmer: klassifisering, regresjon og klyngeanalyse.
Begge metodene kan innebære grafisk fremstilling, men det er primært eksplorativ analyse som søker å generere handlingsrettet innsikt, det vil si innsikt som ansporer beslutningstakere til handling.
Kort sagt, mens utforskende dataanalyse er rettet mot å løse problemer og identifisere løsninger som vil guide de påfølgende modelleringstrinnene, har deskriptiv analyse, som navnet antyder, som hovedmål å gi en detaljert beskrivelse av det aktuelle datasettet.
| Beskrivende analyse | Utforskende dataanalyse |
| Analyserer atferd | Analyserer atferd og forhold |
| Gir en oppsummering | Fører til spesifikasjoner og handlinger |
| Organiserer data i tabeller og grafer | Organiserer data i tabeller og grafer |
| Har begrenset forklaringskraft | Har betydelig forklaringskraft |
Eksempler på praktisk bruk av EDA
#1. Digital markedsføring
Digital markedsføring har utviklet seg fra en kreativ prosess til en datadrevet virksomhet. Markedsføringsorganisasjoner bruker utforskende dataanalyse for å evaluere effekten av kampanjer og for å veilede investerings- og målrettingsbeslutninger.
Demografiske undersøkelser, kundesegmentering og andre teknikker gir markedsførere mulighet til å analysere store mengder data om forbrukerkjøp, undersøkelser og paneldata for å forstå og utforme effektive markedsføringsstrategier.
Nettbaserte analyser gir markedsførere informasjon om interaksjoner på et nettsted på øktnivå. Google Analytics er et eksempel på et gratis analyseverktøy som brukes til dette formålet.
Utforskende teknikker som ofte benyttes innen markedsføring inkluderer modellering av markedsmiks, pris- og markedsføringsanalyser, salgsoptimalisering og utforskende kundeanalyse, som for eksempel segmentering.
#2. Utforskende porteføljeanalyse
En vanlig anvendelse av utforskende dataanalyse er utforskende porteføljeanalyse. En bank eller et utlånsbyrå forvalter en samling av kontoer med varierende verdi og risiko.
Kontoene kan variere basert på innehaverens sosiale status (rik, middelklasse, lavinntekt osv.), geografiske plassering, formue og mange andre faktorer. Utlåner må balansere avkastningen på lån med risikoen for mislighold for hvert lån. Spørsmålet blir da hvordan man vurderer hele porteføljen.
Lånene med lavest risiko kan være knyttet til velstående personer, men det finnes et begrenset antall slike individer. På den andre siden finnes det mange med lav inntekt som kan låne, men dette er forbundet med høyere risiko.
Utforskende dataanalyse kan kombineres med tidsserieanalyse og andre metoder for å bestemme når man skal gi lån til de ulike segmentene av låntakere, og hvilke renter som bør kreves. Rentene beregnes for å dekke tap innenfor det spesifikke segmentet.
#3. Utforskende risikoanalyse
Prediktive modeller innen bank er under utvikling for å gi informasjon om risikovurderinger for individuelle kunder. Kredittscore er utviklet for å forutsi en persons betalingsvilje og brukes ofte til å evaluere kredittverdigheten til den enkelte søker.
I tillegg utføres risikoanalyser innen forskning og forsikringsbransjen. Det er også mye brukt av finansinstitusjoner og betalingsløsningsselskaper for å identifisere legitime og svindelaktige transaksjoner.
Til dette formålet brukes kundens transaksjonshistorikk. Det er vanlig for kortkjøp, hvor kunden blir kontaktet for bekreftelse ved uvanlig høy transaksjonsaktivitet. Dette bidrar til å redusere tap som følge av svindel.
Utforskende dataanalyse med R
For å utføre EDA med R må du først laste ned R base og R Studio (IDE), deretter installere og laste inn følgende pakker:
#Installerer pakker
install.packages("dplyr")
install.packages("ggplot2")
install.packages("magrittr")
install.packages("tsibble")
install.packages("forecast")
install.packages("skimr")
#Laster inn pakker
library(dplyr)
library(ggplot2)
library(magrittr)
library(tsibble)
library(forecast)
library(skimr)
I denne veiledningen vil vi benytte et økonomisk datasett som er inkludert i R, som gir årlige økonomiske indikatorer for amerikansk økonomi. Vi endrer navnet til «econ» for enkelhets skyld:
econ <- ggplot2::economics
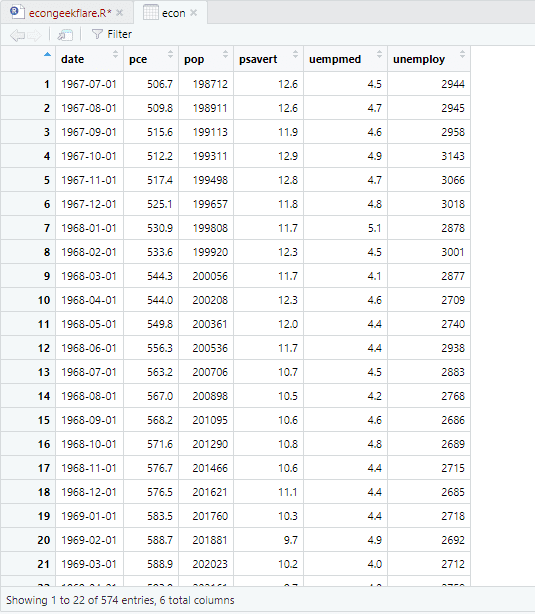
For å gjennomføre beskrivende analyse, bruker vi skimr-pakken, som beregner denne statistikken på en enkel og oversiktlig måte:
#Beskrivende analyse skimr::skim(econ)

Du kan også benytte oppsummeringsfunksjonen for beskrivende analyse:
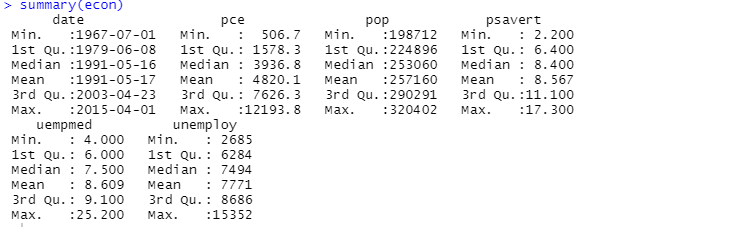
Her vises det at datasettet består av 547 rader og 6 kolonner. Minimumsverdien er fra 1967-07-01, og maksimumsverdien er fra 2015-04-01. I tillegg vises gjennomsnittet og standardavviket.
Nå har du en grunnleggende forståelse av innholdet i «econ»-datasettet. La oss visualisere et histogram for variabelen «uempmed» for å se nærmere på dataene:
#Histogram for arbeidsledighet econ %>% ggplot2::ggplot() + ggplot2::aes(x = uempmed) + ggplot2::geom_histogram() + labs(x = "Arbeidsledighet", title = "Månedlig arbeidsledighet i USA mellom 1967 og 2015")
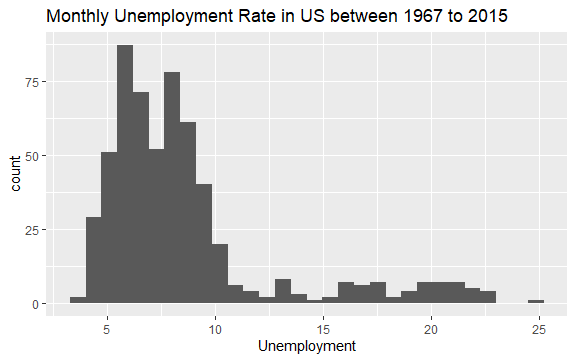
Histogrammet viser at fordelingen har en lang hale til høyre, noe som indikerer at det er noen få observasjoner av denne variabelen med mer «ekstreme» verdier. Spørsmålet er: Når inntraff disse verdiene, og hvordan er trenden i variabelen?
Den mest effektive måten å identifisere trenden for en variabel på er ved hjelp av en linjegraf. Nedenfor genererer vi en linjegraf med en utjevningslinje:
#Linjegraf for arbeidsledighet econ %>% ggplot2::autoplot(uempmed) + ggplot2::geom_smooth()
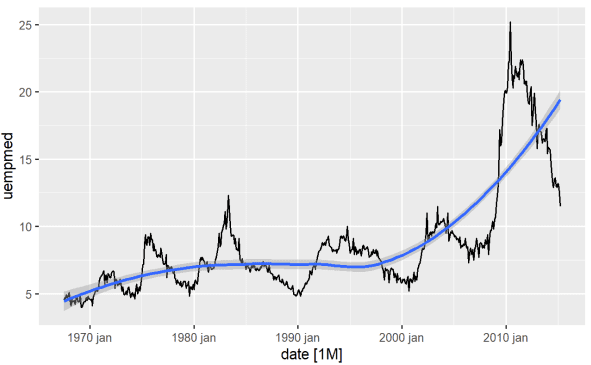
Med denne grafen kan vi se at det i den siste perioden, med de siste observasjonene fra rundt 2010, er en tendens til økende arbeidsledighet, som overgår historiske verdier fra tidligere tiår.
Et annet viktig punkt, spesielt innen økonometrisk modellering, er seriens stasjonaritet, det vil si om gjennomsnittet og variansen er konstante over tid.
Når disse forutsetningene ikke gjelder for en variabel, sier vi at serien har en enhetsrot (ikke-stasjonær), slik at sjokkene variabelen opplever skaper en permanent effekt.
Det ser ut til å være tilfelle for den aktuelle variabelen, varigheten av arbeidsledigheten. Vi har sett at svingningene i variabelen har endret seg betydelig, noe som har store implikasjoner for økonomiske teorier om konjunktursykluser. Men, for å se bort fra teorien, hvordan kan vi i praksis kontrollere om variabelen er stasjonær?
Prognosepakken har en utmerket funksjon for å utføre tester, som ADF, KPSS og andre, som returnerer antall differanser som er nødvendige for at serien skal være stasjonær:
#Bruker ADF-test for å sjekke stasjonaritet forecast::ndiffs( x = econ$uempmed, test = "adf")

Her indikerer en p-verdi større enn 0,05 at dataene ikke er stasjonære.
Et annet viktig aspekt ved tidsserier er identifiseringen av mulige korrelasjoner (det lineære forholdet) mellom de etterslepende verdiene til serien. Korrelogrammene ACF og PACF er nyttige for å identifisere disse.
Siden serien ikke har sesongvariasjoner, men har en viss trend, har de første autokorrelasjonene en tendens til å være store og positive, fordi observasjonene som ligger nært hverandre i tid, også ligger nært hverandre i verdi.
Derfor vil autokorrelasjonsfunksjonen (ACF) for en trendet tidsserie tendere mot å ha positive verdier som gradvis avtar med økende etterslep.
#Residualer for arbeidsledighet checkresiduals(econ$uempmed) pacf(econ$uempmed)
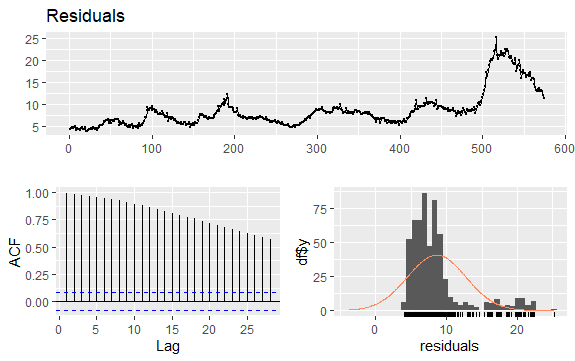
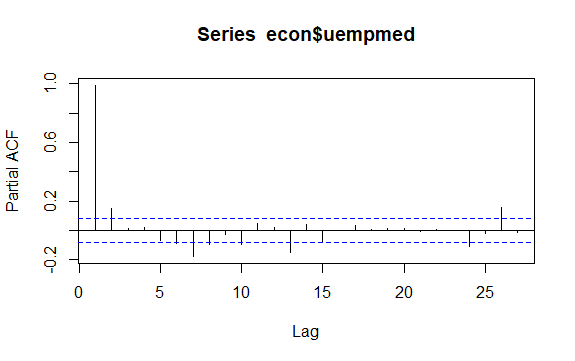
Konklusjon
Når vi arbeider med datasett som er mer eller mindre «rene», det vil si allerede bearbeidet, kan det være fristende å hoppe direkte til modellbyggingsfasen for å få de første resultatene. Det er viktig å motstå denne fristelsen og starte med utforskende dataanalyse, som er enkelt, men likevel gir oss verdifull innsikt i dataene.
Det kan også være nyttig å undersøke noen av de beste ressursene for å lære statistikk for datavitenskap.