Å implementere søkefunksjonalitet er alltid en utfordring, men absolutt ikke en umulighet.
I det virkelige liv søker vi sjelden etter et forutbestemt mønster. Vi leter instinktivt på de stedene der vi anser det som mest sannsynlig at det vi leter etter befinner seg. Vi følger ikke noe spesifikt skjema i de fleste tilfeller.
Fungerer det samme prinsippet innenfor programmering?
Nei, i programmering er det nødvendig med en strukturert fremgangsmåte for å lokalisere elementer. I denne artikkelen skal vi utforske ulike algoritmer som benytter seg av forskjellige søkemønstre.
Det finnes mange søkealgoritmer i programmeringsverdenen. Vi skal fokusere på de mest sentrale og mest brukte i denne artikkelen. Når du forstår disse, vil resten av algoritmene være enklere å lære.
I denne artikkelen refererer «søking» til prosessen med å finne et bestemt element i en array.
La oss se nærmere på disse algoritmene.
Lineært Søk
Som navnet antyder, følger lineær søkealgoritme et lineært mønster når den søker etter elementer i en array. Algoritmen starter fra begynnelsen av arrayet og beveger seg sekvensielt mot slutten, helt til den finner det ønskede elementet. Når elementet er funnet, avsluttes programutførelsen.
For å illustrere hvordan lineært søk fungerer, kan vi se på noen eksempler for å få en bedre forståelse av algoritmen.
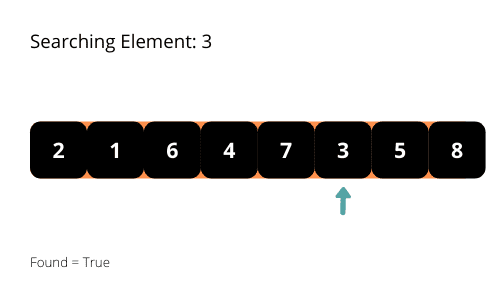
Ved å observere søkemønsteret nøye, vil vi se at den maksimale tiden det tar for algoritmen å kjøre er O(n), også kalt «worst-case» tidskompleksitet. Når vi analyserer algoritmer, er det vanlig å vurdere den verst tenkelige tidskompleksiteten. Derfor er tidskompleksiteten for lineært søk O(n).
La oss se hvordan vi implementerer en lineær søkealgoritme.
Implementering av Lineært Søk
Nå som du har en god forståelse av hvordan lineær søkealgoritme fungerer, er det på tide å prøve seg på litt kode. Først skal vi gå gjennom trinnene for å implementere lineært søk, slik at du deretter kan forsøke å kode det selv. Ikke bekymre deg hvis du ikke lykkes i første forsøk, vi vil gå gjennom koden etterpå.
Her er stegene for å implementere en lineær søkealgoritme:
- Opprett en array med elementer (dine favorittall).
- Definer en funksjon kalt «search_element» som tar tre argumenter: arrayet, lengden av arrayet og elementet du søker etter.
- Funksjonen «search_element(arr, n, element)»:
- Iterer gjennom det angitte arrayet.
- For hvert element, sjekk om det er lik elementet vi leter etter.
- Hvis det er likt, returner «True».
- Hvis løkken fullføres uten å finne elementet, betyr det at elementet ikke finnes i arrayet. Returner derfor «False».
- Iterer gjennom det angitte arrayet.
- Skriv ut en melding basert på returverdien fra funksjonen «search_element».
Bruk nå disse trinnene til å skrive kode for å implementere den lineære søkealgoritmen.
Har du implementert den lineære søkealgoritmen? Utmerket! La oss dobbeltsjekke med koden nedenfor.
Hvis du ikke klarte det, ikke bekymre deg, ta en titt på koden under og se hvordan vi har implementert den. Du vil få taket på det ganske enkelt.
## søkefunksjon def search_element(arr, n, element): ## itererer gjennom arrayet for i in range(n): ## sjekker det gjeldende elementet med ønsket element if arr[i] == element: ## returnerer True ved treff return True ## elementet finnes ikke, så utførelsen kommer hit return False if __name__ == '__main__': ## initialiserer arrayet, lengden og elementet som skal søkes arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 6 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "er funnet") else: print(element_to_be_searched, "er ikke funnet")
Kjør først programmet med et element som finnes i arrayet, og deretter med et element som ikke finnes.
Tidskompleksiteten til den lineære søkealgoritmen er O(n).
Kan vi redusere dette ytterligere med andre metoder?
Ja, det kan vi. La oss se hvordan.
Binært Søk
Binær søkealgoritme sjekker alltid midtelementet i en array. Denne algoritmen brukes kun for å søke i sorterte arrayer.
Binær søkealgoritme itererer gjennom arrayet, sjekker midtelementet, og avsluttes hvis elementet er funnet. Hvis det midterste elementet er mindre enn det elementet vi leter etter, ekskluderer algoritmen den venstre delen av arrayet (inkludert midtelementet) fra videre søk. Hvis det midterste elementet er større enn det elementet vi leter etter, ekskluderer den den høyre delen av arrayet (inkludert midtelementet) fra videre søk.
I hver iterasjon reduserer binær søkealgoritme området det søker i. Derfor kreves det færre kontroller sammenlignet med lineær søkealgoritme.
La oss se på noen illustrasjoner som kan hjelpe oss å forstå binær søkealgoritme bedre.
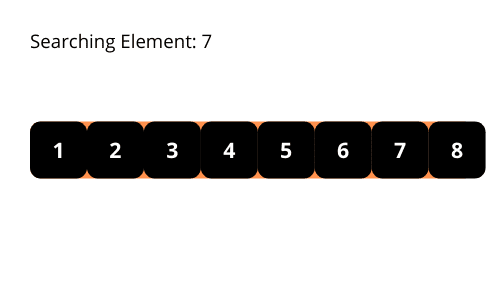
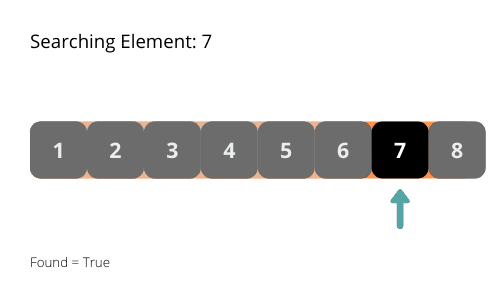
Tidskompleksiteten for binær søkealgoritme er O(log n). I hver iterasjon halveres lengden på søkeområdet, noe som resulterer i en eksponentiell reduksjon.
Implementering av Binært Søk
Først ser vi på trinnene for å implementere binær søkealgoritme, og deretter går vi gjennom koden. Her er trinnene for å implementere binær søkealgoritme:
- Opprett en array med elementer (dine favorittall).
- Lag en funksjon kalt «search_element», som tar tre argumenter: et sortert array, lengden av arrayet og elementet du søker etter.
- Funksjonen «search_element(sortert_arr, n, element)»:
- Initialiser en indeksvariabel «i» for array-iterasjon.
- Initialiser to variabler, «start» og «slutt», for å holde oversikt over søkeområdet. Disse representerer start- og sluttindeksene.
- Iterer så lenge «i» er mindre enn lengden på arrayet.
- Beregn midtindeksen for søkeområdet ved hjelp av «start» og «slutt» verdiene: (start + slutt) // 2.
- Sjekk om elementet i midtindeksen er lik elementet du leter etter.
- Hvis de er like, returner «True».
- Hvis midtindeks elementet er mindre enn elementet du leter etter, flytt «start»-indeksen til midten + 1.
- Hvis midtindeks elementet er større enn elementet du leter etter, flytt «slutt»-indeksen til midten – 1.
- Øk array-indeksen «i».
- Hvis loopen er fullført uten at elementet er funnet, betyr det at elementet ikke finnes i arrayet. Returner derfor «False».
- Skriv ut en melding basert på returverdien fra funksjonen «search_element».
Prøv å skrive koden basert på implementeringen for lineært søk.
…
Fikk du til koden?
Hvis ja, sjekk den mot koden nedenfor. Hvis ikke, ikke bekymre deg; la oss gå gjennom implementasjonen sammen med koden nedenfor.
## søkefunksjon def search_element(sorted_arr, n, element): ## array-indeks for iterasjon i = 0 ## variabler for å spore søkeområdet ## initialiserer dem med start- og sluttindekser start = 0 end = n - 1 ## itererer gjennom arrayet while i < n: ## henter indeksen for midtelementet middle = (start + end) // 2 ## sjekker midtelementet mot elementet som søkes if sorted_arr[middle] == element: ## returnerer True siden elementet finnes i arrayet return True elif sorted_arr[middle] < element: ## flytter startindeksen for søkeområdet mot høyre start = middle + 1 else: ## flytter sluttindeksen for søkeområdet mot venstre end = middle - 1 i += 1 return False if __name__ == '__main__': ## initialiserer arrayet, lengden og elementet som skal søkes arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] n = 10 element_to_be_searched = 9 # element_to_be_searched = 11 if search_element(arr, n, element_to_be_searched): print(element_to_be_searched, "er funnet") else: print(element_to_be_searched, "er ikke funnet")
Test koden med forskjellige scenarier der elementet er tilstede og ikke tilstede i arrayet.
Konklusjon
Binær søkealgoritme er mye mer effektiv enn lineær søkealgoritme. En forutsetning for binær søkealgoritme er at arrayet er sortert, noe som ikke er nødvendig for lineær søkealgoritme. Sortering tar tid, men effektive sorteringsalgoritmer i kombinasjon med binært søk vil gi et godt resultat.
Nå har du en god forståelse av de mest brukte søkealgoritmene i Python.
Du kan utforske mer om populær, selv-hostet søkeprogramvare.
Lykke til med kodingen! 🙂 🧑💻