Forstå Flyttall i Python
En av de mest brukte datatypene i Python er flyt, som benyttes for å representere desimaltall. Disse tallene, både positive og negative, karakteriseres ved at de inneholder en desimaldel. Flyttall omfatter også tall som er uttrykt i vitenskapelig notasjon, hvor bokstaven «e» eller «E» indikerer en potens av 10.
Datatypen float er essensiell fordi den muliggjør representasjon av et bredt spekter av reelle tall, fra svært små til enorme verdier.

Her er eksempler på hvordan flyttall ser ut i Python:
# eksempler på flyttall a = 20.0 b = -51.51345 c = 65e7 d = -1.08E12 e = 2E10 print(type(a)) print(type(b)) print(type(c)) print(type(d)) print(type(e))
Output:
<class 'float'> <class 'float'> <class 'float'> <class 'float'> <class 'float'>
Flyttall muliggjør mer presise beregninger sammenlignet med datatyper som heltall, hvor desimaldelen av et tall blir ignorert. For eksempel, et tall som 3.142 vil med heltall kun bli representert som 3.
Med flyttall, derimot, vil tallet bli representert nøyaktig slik det er, altså 3.142. Dette gjør flyttall bedre egnet for matematiske operasjoner som krever høy grad av nøyaktighet.
Flytende tall er svært anvendelige i en rekke felter, inkludert reell modellering, maskinlæring, dataanalyse, økonomi, matematiske beregninger, grafikk, visualisering og vitenskapelige utregninger.
Heltall kontra Flyttall i Python
Heltall, representert som «int» i Python, er en annen fundamentalt viktig datatype. I motsetning til flyttall, har heltall ingen desimaldel. De består av positive hele tall, negative hele tall og null.
Heltall er ideelle for operasjoner som involverer hele tall, som for eksempel telling og indeksering.
Her er noen eksempler på heltall:
a = 0 b = 968 c = -14 print(type(a)) print(type(b)) print(type(c))
Output:
<class 'int'> <class 'int'> <class 'int'>
De viktigste forskjellene mellom heltall og flyttall oppsummeres i tabellen nedenfor:
| Karakteristikk | Heltall (int) | Flyttall (float) |
| Representasjon | Hele tall, negative motstykker, og null, uten desimaler. | Reelle tall med desimalpunkt. |
| Presisjon | Ubegrenset presisjon, kun begrenset av tilgjengelig minne. | Begrenset presisjon, med en maksimal verdi på ca. 1.8 x 10308. |
| Minnebruk | Bruker mindre minne enn flyttall. | Bruker mer minne enn heltall. |
| Bitvise operasjoner | Vanlig brukt i bitvise operasjoner. | Sjelden brukt i bitvise operasjoner. |
| Anvendelse | Brukes i telling, indeksering, og bitvise operasjoner. | Brukes i målinger og matematiske beregninger. |
Forskjellige Måter å Opprette og Bruke Flyttall i Python
Den enkleste måten å arbeide med flyttall er ved å tilordne en variabel en flytverdi direkte:
# tilordne en variabel en flytverdi a = 3.142
En annen metode for å generere flyttall er ved å konvertere heltall eller numeriske strenger ved hjelp av `float()`-konstruktøren. Ved å sende inn en heltallsverdi eller en streng til `float()`, vil den konverteres til en tilsvarende flytverdi:
number1 = 2524 numString1 = "513.523" numString2 = "1341" # Konverter til float og lagre verdien i en variabel a = float(number1) print(a) b = float(numString1); print(b) c = float(numString2) print(c)
Output:
2524.0 513.523 1341.0
I eksemplet over konverteres både heltall og strenger til float ved hjelp av `float()`, og deretter lagres de i en variabel før de skrives ut, noe som demonstrerer de resulterende flytverdiene etter konverteringen.
Flyttall kan også oppstå som resultat av matematiske beregninger, for eksempel divisjon:
num1 = 20
num2 = 3
result = num1/num2
print("Resultatet av divisjonen som et heltall:")
print(int(20/3))
print("Resultatet av divisjonen som en flytverdi:")
print(result)
print(type(result))
Output:
Resultatet av divisjonen som et heltall: 6 Resultatet av divisjonen som en flytverdi: 6.666666666666667 <class 'float'>
Dette eksemplet illustrerer hvordan flyttall gir et mer nøyaktig svar sammenlignet med heltallsdivisjon, som avrunder resultatet ned til nærmeste heltall.
Når du arbeider med flyttall i Python, kan du støte på uventede resultater på grunn av hvordan flyttall representeres internt i datamaskinen. Flyttall representeres i maskinvare som binære brøker, med grunntall 2.
Imidlertid kan ikke de fleste desimalbrøker, spesielt de med gjentagende desimaler, representeres nøyaktig som en binær brøk. Som en konsekvens blir flyttall vanligvis lagret som en tilnærming av den faktiske verdien.
For å illustrere dette, se på flytverdien 0.3. Hvis du tilordner 0.3 til en variabel, vil den ikke lagres nøyaktig som 0.3 internt. Dette kan vises ved hjelp av `format()`-funksjonen, som lar oss se hvordan en verdi representeres med et spesifisert antall signifikante sifre. I eksemplet under, viser vi 0.3 med 20 signifikante sifre:
num = 0.3
print("num med 20 signifikante sifre")
print(format(num, '.20f'))
print("Verdien vi lagret for num")
print(num)
Output:
num med 20 signifikante sifre 0.29999999999999998890 Verdien vi lagret for num 0.3
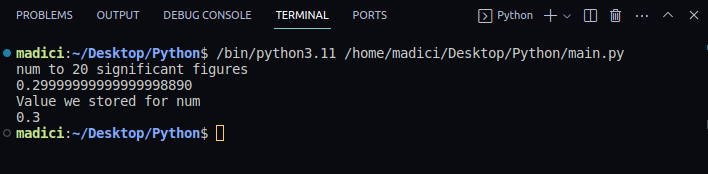
Som vist, lagres ikke verdien 0.3 nøyaktig som 0.3 internt. Når variabelen `num` printes, får vi en avrundet verdi.
Dette kan føre til uventede resultater når du utfører operasjoner med flyttall. For eksempel, en manuell beregning av 0.3 + 0.3 + 0.3 vil gi 0.9, men dette er ikke nødvendigvis tilfelle i Python, siden den lagrer binære tilnærminger av den faktiske verdien. Dette vises under:
sum = 0.3 + 0.3 + 0.3
answer = 0.9
print("Er sum lik svaret: ")
print(sum == answer)
print("Den interne representasjonen av sum er: ")
print(sum)
print("Svaret fra manuell beregning er: ")
print(answer)
Output:
Er sum lik svaret: False Den interne representasjonen av sum er: 0.8999999999999999 Svaret fra manuell beregning er: 0.9
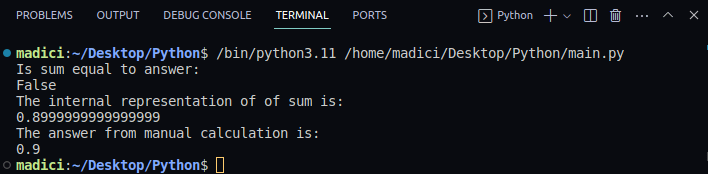
Det er viktig å være oppmerksom på at Python ikke lagrer eksakte flytverdier internt, men tilnærminger. Derfor, når du sammenligner flyttall, bør du vurdere å runde av til samme antall signifikante sifre. For økt nøyaktighet, bruk den innebygde `decimal`-modulen.
`decimal`-modulen i Python
I situasjoner der høy nøyaktighet er avgjørende, som i finansielle og vitenskapelige beregninger, er flyttall ikke ideelt. For å garantere høy nøyaktighet, bør du benytte `decimal`-modulen, en del av Pythons standardbibliotek.
I motsetning til `float`, som lagres som binære flyttall, bruker `decimal`-modulen en maskinuavhengig desimalbasert representasjon. Dette gir høyere presisjon ved at desimaltall kan representeres nøyaktig som de er, samt at de kan brukes nøyaktig i beregninger. I tillegg tilbyr `decimal`-modulen presis avrunding.
For å bruke `decimal`-modulen, må du importere den:
import decimal
For å demonstrere fordelene med `decimal`-modulen, la oss gjenta den tidligere sammenligningen av summen 0.3 + 0.3 + 0.3 med verdien 0.9:
import decimal
sum = decimal.Decimal('0.3') + decimal.Decimal('0.3') + decimal.Decimal('0.3')
answer = decimal.Decimal('0.9')
print("Er sum lik svaret: ")
print(sum == answer)
print("Den interne representasjonen av sum er: ")
print(sum)
print("Svaret fra manuell beregning er: ")
print(answer)
Output:
Er sum lik svaret: True Den interne representasjonen av sum er: 0.9 Svaret fra manuell beregning er: 0.9
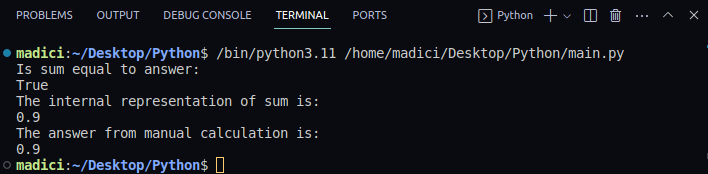
Dette eksemplet viser hvordan `decimal`-modulen håndterer flyttall med presisjon, og gir det forventede resultatet. Derfor, når du jobber med flyttall og trenger høy nøyaktighet, bør du alltid bruke `decimal`-modulen.
Vanlige Feil ved Bruk av Flyttall
Mange feil som oppstår når man arbeider med flyttall i Python, stammer fra manglende forståelse av hvordan flyttall representeres internt. For eksempel vil en verdi som 0.3 ikke lagres nøyaktig som 0.3. Derfor vil du sannsynligvis støte på feil hvis du antar at flyttall lagres eksakt.

En vanlig feil er avrundingsfeilen som oppstår når du utfører matematiske operasjoner på flyttall. Siden Python ikke kan representere flytverdier nøyaktig, kan du støte på avrundingsfeil der resultatene kanskje ikke er som forventet.
Disse avrundingsfeilene kan også føre til feil når du forsøker å gjøre sammenligninger mellom flytverdier. Vær derfor ekstra forsiktig når du jobber med flyttall og vær oppmerksom på at uventede utfall kan forekomme.
Den beste måten å unngå disse feilene er å bruke `decimal`-modulen. Ved å gjøre dette, vil resultatene av dine beregninger være mer forutsigbare og nøyaktige.
Konklusjon
Som Python-programmerer er det essensielt å forstå hvordan flyt-datatypen fungerer. For å unngå feil, er det viktig å vite hvordan Python representerer flyttall internt. Unngå derfor å gjøre eksakte likhetssammenligninger med flyttall, da dette kan føre til feil.
Dersom nøyaktighet er avgjørende i applikasjonen din, bør du unngå flyt-datatypen og heller bruke `decimal`-modulen. Denne modulen sikrer nøyaktige flyttallresultater og representerer tallene presist og på en maskinuavhengig måte.
Du kan også være interessert i å lese om Python Itertools Functions og Python Try Except.