Helt siden den spede starten med den første ideen om en kvantedatamaskin i 1980, har kvantedataområdet vokst betraktelig, spesielt det siste tiåret. Et stort antall selskaper er nå involvert i utviklingen av kvantedatamaskiner.
Kvanteberegning kan virke vanskelig å forstå for de fleste. Mye av den eksisterende informasjonen unnlater ofte å forklare de grunnleggende detaljene på en klar måte.
Denne artikkelen har som mål å gjøre kvanteberegning forståelig. Ved å lese hele artikkelen, vil du få en omfattende oversikt over hva kvanteberegning er, de ulike typene av kvanteberegning, deres funksjoner, algoritmer, modeller, tilnærminger, utfordringer og potensielle bruksområder.
Hva er kvantedatamaskiner?
Kvantedatamaskiner tar i bruk en annen tilnærming til problemløsning enn de datamaskinene vi er vant til, som jeg fra nå av vil omtale som klassiske datamaskiner.
Kvantedatamaskiner har visse fordeler over vanlige datamaskiner for spesifikke typer problemer. Disse fordelene springer ut fra deres evne til å eksistere i mange tilstander samtidig, i motsetning til klassiske datamaskiner som bare kan være i én tilstand om gangen.
 Bildekilde: IBM
Bildekilde: IBM
For å forstå hvordan kvantedatamaskiner fungerer, må vi se nærmere på tre begreper: Superposisjon, sammenfiltring og interferens.
I en vanlig datamaskin brukes biter som den grunnleggende enheten, mens kvantedatamaskiner benytter kvantebiter, eller qubits. Disse to opererer på fundamentalt forskjellige måter.
En klassisk bit fungerer som en bryter som kan være enten 0 eller 1, som du kanskje kjenner som binær informasjon. Når vi måler en bit, får vi bare tilbake den tilstanden den er i for øyeblikket. Dette gjelder ikke for qubits, som er mer komplekse.
Superposisjon
For å visualisere dette kan du tenke på en qubit som en pil som peker i et 3D-rom. Hvis pilen peker opp, er den i 1-tilstanden. Hvis den peker ned, er den i 0-tilstanden, akkurat som en klassisk bit. Men den har også muligheten til å være i en såkalt superposisjonstilstand, som oppstår når pilen peker i en hvilken som helst annen retning.
Denne superposisjonstilstanden er en kombinasjon av 0 og 1.
 Superposisjonsstat
Superposisjonsstat
Når vi måler en qubit, vil resultatet fortsatt være enten 1 eller 0, men hvilken av dem vi får avhenger av en sannsynlighet som bestemmes av pilens retning.
Hvis pilen peker mer oppover, er det mer sannsynlig at vi får 1 enn 0. Hvis den peker mer nedover, er det mer sannsynlig at vi får 0 enn 1. Hvis den peker rett ut fra ekvator, er det 50 % sjanse for å få begge tilstandene.
Dette er en forklaring på superposisjon. La oss nå gå videre til sammenfiltring.
Sammenfiltring
I klassiske datamaskiner er bitene helt uavhengige av hverandre. Tilstanden til en bit påvirkes ikke av tilstanden til noen av de andre bitene. I kvantedatamaskiner kan qubits derimot være sammenfiltret, noe som betyr at de blir en del av én enkelt kvantetilstand.
La oss se på to qubits som hver er i forskjellige superposisjonstilstander, men ikke er sammenfiltret ennå. Du kan se sannsynlighetene ved siden av dem, og disse sannsynlighetene er for øyeblikket uavhengige av hverandre.
Når vi filtrer dem sammen, må vi kaste de uavhengige sannsynlighetene og beregne en sannsynlighetsfordeling for alle mulige tilstander vi kan få ut: 00, 01, 10 eller 11.

Det viktigste her er at når qubits er sammenfiltret, vil en endring i pilens retning på en qubit endre sannsynlighetsfordelingen for hele systemet. Qubits er ikke lenger uavhengige av hverandre, men er en del av en større tilstand.
Dette gjelder uansett hvor mange qubits vi har. For én qubit har vi en sannsynlighetsfordeling over to tilstander.
Med to qubits har vi en sannsynlighetsfordeling over fire tilstander. Med tre qubits har vi en fordeling over åtte tilstander, og dette tallet dobles hver gang vi legger til en ny qubit.
Generelt kan en kvantedatamaskin med n qubits være i en kombinasjon av 2^n tilstander. Dette er den grunnleggende forskjellen mellom klassiske datamaskiner og kvantedatamaskiner.

Klassiske datamaskiner kan være i hvilken som helst tilstand, men bare én om gangen, mens kvantedatamaskiner kan være i en superposisjon av alle disse tilstandene samtidig.
Men hvordan kan det å være i denne superposisjonstilstanden være nyttig? For å forstå det trenger vi den siste komponenten: Interferens.
Interferens
For å forklare effekten av interferens, må vi se nærmere på bildet av en qubit som teknisk sett kalles en Bloch-sfære. En qubit ser ikke egentlig slik ut; dette er bare en visuell måte å representere tilstanden til en qubit.
I virkeligheten beskrives tilstanden til en qubit av en mer abstrakt enhet kalt en kvantebølgefunksjon. Bølgefunksjoner er den grunnleggende matematiske beskrivelsen av alt innen kvantemekanikk.
Når mange qubits er sammenfiltret, legges alle deres bølgefunksjoner sammen til en samlet bølgefunksjon som beskriver tilstanden til kvantedatamaskinen.
Denne sammenslåingen av bølgefunksjoner er interferensen. Akkurat som med bølger på vann, kan de legge seg sammen konstruktivt og danne en større bølge, eller destruktivt og kansellere hverandre.
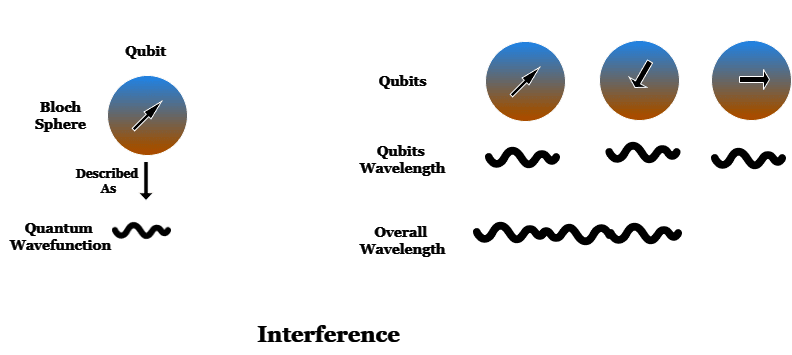
Den samlede bølgefunksjonen til kvantedatamaskinen er det som definerer de ulike sannsynlighetene for de ulike tilstandene. Ved å endre tilstandene til de ulike qubitene kan vi endre sannsynligheten for at ulike tilstander vil bli avslørt når vi måler kvantedatamaskinen.
Husk at selv om kvantedatamaskinen kan være i en superposisjon av millioner av tilstander samtidig, får vi bare én enkelt tilstand når vi måler den.
Når vi bruker en kvantedatamaskin for å løse et problem, må vi bruke konstruktiv interferens for å øke sannsynligheten for det riktige svaret og destruktiv interferens for å redusere sannsynligheten for de feile svarene, slik at vi får det riktige svaret når vi måler.
Kvantealgoritmer
Måten vi gjør dette på, er innenfor feltet kvantealgoritmer. Selve motivasjonen bak kvanteberegning er at det i teorien er mange problemer som kan løses med en kvantedatamaskin, men som anses som svært vanskelige å løse med klassiske datamaskiner.
La oss se nærmere på noen av disse algoritmene. Det finnes mange kvantealgoritmer, så vi skal fokusere på de mest kjente og historisk viktige: Shors algoritme.
#1. Shors algoritme
Hvis du har to store tall og multipliserer dem sammen, finnes det en rask og effektiv klassisk algoritme for å finne svaret. Men hvis du starter med svaret og spør hvilke tall som er multiplisert for å få dette tallet, er det mye vanskeligere.
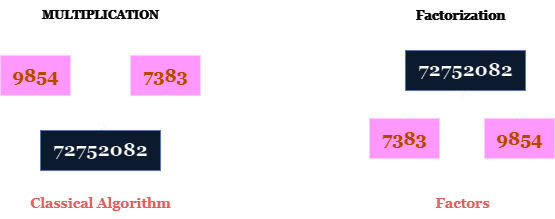
Dette kalles faktorisering, og tallene kalles faktorer. Det er vanskelig å finne dem fordi søkerommet for mulige faktorer er så stort. Det finnes ingen effektiv klassisk algoritme for å finne faktorene til store tall.
Denne matematiske egenskapen brukes til internettkryptering for å sikre nettsteder, e-poster og bankkontoer. Hvis vi kjenner disse faktorene, kan vi enkelt dekryptere informasjonen, men hvis vi ikke gjør det, må vi først finne dem, noe som er svært vanskelig, selv for verdens kraftigste datamaskiner.
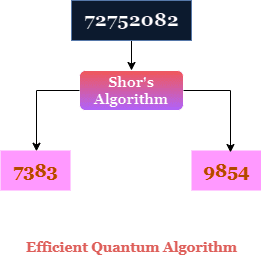 Shors algoritme
Shors algoritme
Derfor vakte det stor oppsikt i 1994 da Peter Shor publiserte en rask kvantealgoritme som effektivt kunne finne faktorene til store heltall.
Dette var et vendepunkt, da mange begynte å ta ideen om kvanteberegning på alvor. Det var den første applikasjonen på et problem i den virkelige verden med potensielt store sikkerhetsimplikasjoner.
Men hvor rask er en «rask» kvantealgoritme? Hvor mye raskere enn en klassisk datamaskin ville den være? For å svare på det må vi se litt nærmere på kvantekompleksitetsteori.
Kvantekompleksitetsteori
Kvantekompleksitetsteori er en underkategori av beregningskompleksitetsteori, som handler om å kategorisere algoritmer og sortere dem i grupper etter hvor godt de fungerer på datamaskiner.
Klassifiseringen bestemmes av vanskelighetsgraden for å løse et problem etter hvert som det blir større. I P-boksen er alle problemer enkle å løse for klassiske datamaskiner, men alt utenfor denne boksen betyr at vi ikke har effektive klassiske algoritmer for å løse dem. Faktorisering av store tall er en av disse.
Det finnes en annen sirkel kalt BQP, som er effektiv for en kvantedatamaskin, men ikke for en klassisk datamaskin. Dette er problemene som kvantedatamaskiner vil være bedre til å løse enn klassiske datamaskiner.
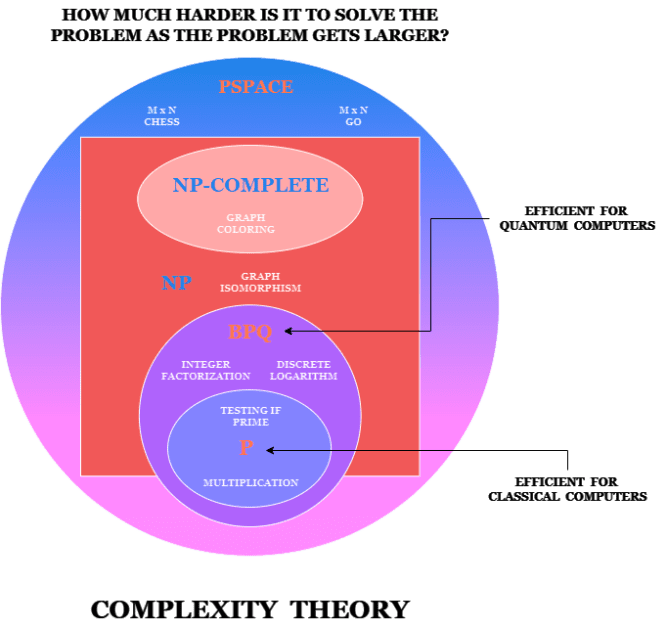
Som nevnt ser kompleksitetsteori på hvor vanskelig det er å løse et problem etter hvert som problemet vokser. Hvis du faktoriserer et tall med 8 sifre og legger til ett siffer til, hvor mye vanskeligere er det å faktorisere det nye tallet sammenlignet med det gamle? Er det dobbelt så vanskelig?
Er det eksponentielt vanskeligere? Og hva er trenden når vi legger til flere og flere sifre? Dette kalles kompleksitet eller skalering. For faktorisering er den eksponentiell.
Alt med N i eksponenten er eksponentielt vanskelig. Disse eksponentielle problemene er de som vokser kraftig etter hvert som problemene vokser. I datavitenskap kan du oppnå respekt og berømmelse hvis du finner en bedre algoritme for å løse disse vanskelige problemene.
Et eksempel på dette er Shors algoritme, som utnytter de spesielle funksjonene til kvantedatamaskiner til å lage en algoritme som kan løse heltallsfaktorisering med en skalering som er mye bedre enn den beste klassiske algoritmen.
Den beste klassiske algoritmen er eksponentiell, mens Shors algoritme er polynom, som er en enorm forskjell i kompleksitetsteori og datavitenskap generelt. Den forvandler et uløselig problem til et løsbart problem.
Løsbart vil si at hvis du har en fungerende kvantedatamaskin, noe det jobbes hardt med å bygge. Du trenger ikke å bekymre deg for sikkerheten til bankkontoen din ennå, for dagens kvantedatamaskiner kan ennå ikke kjøre Shors algoritme på store tall.

IBM Quantum
De trenger et stort antall qubits for å gjøre dette, men de mest avanserte universelle kvantedatamaskinene har per i dag omtrent 433.
Det jobbes også med det som kalles post-kvantekrypteringssystemer, som ikke bruker heltallsfaktorisering. I tillegg kan kvantekryptografi, som er en annen teknologi fra kvantefysikken, hjelpe her.
Dette var en gjennomgang av bare én kvantealgoritme. Det finnes mange flere, hver med ulike hastigheter.
#2. Grovers algoritme
Et annet bemerkelsesverdig eksempel er Grovers algoritme, som kan søke i ustrukturerte lister over data raskere enn den beste klassiske algoritmen.
Vi bør imidlertid være forsiktige slik at vi ikke feilkarakteriserer klassiske datamaskiner. De er svært allsidige verktøy, og det er ingenting i veien for at noen kan finne en svært smart klassisk algoritme som kan løse de vanskeligste problemene, som heltallsfaktorisering, mer effektivt.
Dette er usannsynlig, men ikke umulig. Det finnes også problemer som det er bevist at er umulige å løse på klassiske datamaskiner, kalt ikke-beregnbare problemer, som stoppeproblemet. Disse er også umulige å løse på en kvantedatamaskin.
Beregningsmessig er klassiske datamaskiner og kvantedatamaskiner ekvivalente med hverandre. Forskjellen ligger i algoritmene de kan kjøre. Du kan til og med simulere en kvantedatamaskin på en klassisk datamaskin og omvendt.
Simulering av en kvantedatamaskin på en klassisk datamaskin blir eksponentielt mer utfordrende etter hvert som antallet qubits som simuleres øker.
Dette er fordi klassiske datamaskiner sliter med å simulere kvantesystemer, men ettersom kvantedatamaskiner allerede er kvantesystemer, har de ikke dette problemet. Dette leder oss over til den mest interessante anvendelsen av kvantedatamaskiner: kvantesimulering.
#3. Kvantesimulering
Kvantesimulering innebærer å simulere ting som kjemiske reaksjoner eller elektroners oppførsel i ulike materialer ved hjelp av en datamaskin. Kvantedatamaskiner har her også en eksponentiell fordel over klassiske datamaskiner, ettersom klassiske datamaskiner har vanskeligheter med å simulere kvantesystemer.
Det er vanskelig å simulere kvantesystemer selv med noen få partikler, selv på verdens kraftigste superdatamaskiner. Vi kan heller ikke gjøre dette på kvantedatamaskiner ennå. Men etter hvert som teknologien modnes, er målet å simulere større og større kvantesystemer.
Dette inkluderer områder som oppførsel til eksotiske materialer ved lave temperaturer. For eksempel å finne ut hva som gjør at noen materialer blir superledende eller å studere viktige kjemiske reaksjoner for å forbedre deres effektivitet. Ett prosjekt tar sikte på å produsere gjødsel på en måte som frigjør mye mindre karbondioksid, ettersom gjødselproduksjon står for omtrent 2 % av de globale karbonutslippene.
Du kan lære mer om kvantekjemisk simulering.

Kvantesimulering
Andre potensielle bruksområder for kvantesimulering inkluderer forbedring av solcellepaneler, forbedring av batterier og utvikling av nye medisiner, kjemikalier eller materialer for romfart.
Generelt vil kvantesimulering bety at vi raskt kan lage prototyper av mange ulike materialer i en kvantedatamaskin og teste alle deres fysiske parametere, i stedet for å måtte fysisk lage dem og teste dem i et laboratorium. Sistnevnte er en mye mer krevende og kostbar prosess.
Dette kan i stor grad fremskynde prosesser og gi betydelige tids- og kostnadsbesparelser. Det er viktig å gjenta at dette er potensielle bruksområder for kvantedatamaskiner. Vi har ikke kvantedatamaskiner som kan løse reelle problemer bedre enn vanlige datamaskiner ennå. Dette er imidlertid den typen problemer kvantedatamaskiner ville være godt egnet til.
Modeller av kvantedatamaskiner

Innenfor kvantedatamaskinenes verden finnes et stort spekter av tilnærminger til hvordan man kan gjøre ulike kvantesystemer om til kvantedatamaskiner. Det er to nivåer av detaljer jeg må nevne her.
Kretsmodellen
I kretsmodellen har vi qubits som jobber sammen og spesielle porter som endrer tilstanden til et par qubits om gangen, uten å sjekke dem. Disse portene settes i en bestemt rekkefølge for å lage en kvantealgoritme. Til slutt måles qubitene for å få det ønskede svaret.
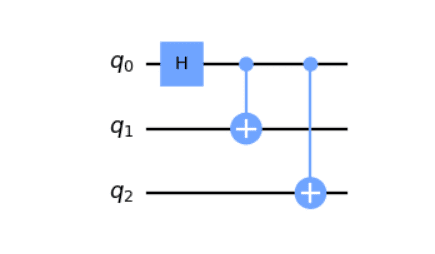 Bildekreditt: qiskit
Bildekreditt: qiskit
Adiabatisk kvanteberegning
Adiabatisk kvanteberegning drar nytte av et grunnleggende prinsipp i fysikk: at ethvert system alltid beveger seg mot sin minimumsenergitilstand. Adiabatisk kvanteberegning fungerer ved å omformulere problemer slik at kvantesystemets laveste energitilstand representerer løsningen.
Kvanteglødning
Kvanteglødning er ikke et universelt kvanteberegningssystem, men fungerer etter samme prinsipp som adiabatisk kvanteberegning. Systemet prøver å finne minimumsenergitilstanden til et energilandskap som du angir.
Topologisk kvanteberegning
I denne tilnærmingen bygges qubits av en enhet i fysikk som kalles en Majorana nullmodus kvasi-partikkel, som er en type ikke-abelsk anyon. Det er forutsagt at disse kvasi-partiklene er mer stabile på grunn av deres fysiske separasjon fra hverandre.
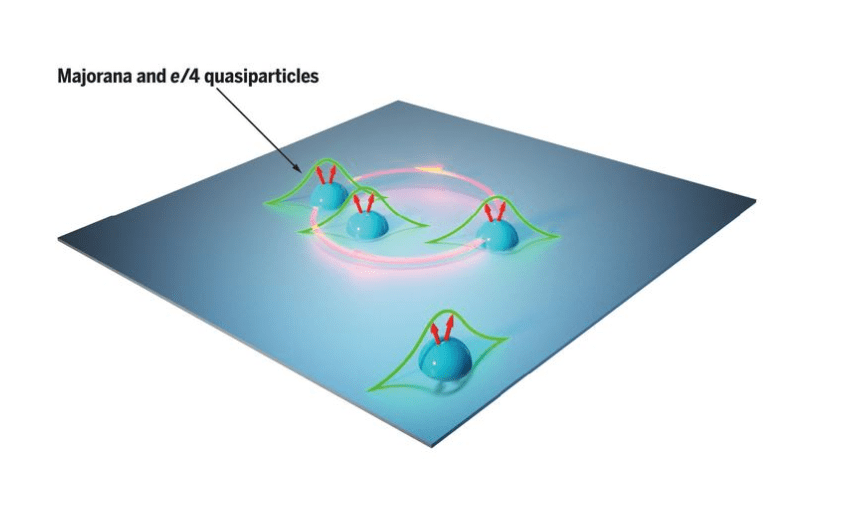 Bildekreditt Sivilt daglig
Bildekreditt Sivilt daglig
Utfordringer ved bygging
Uavhengig av tilnærming, er det noen felles hindringer vi må se nærmere på.
- Dekoherens: Det er veldig vanskelig å kontrollere kvantesystemer. Hvis det oppstår en liten interaksjon med omverdenen, begynner informasjonen å lekke bort. Dette kalles dekoherens. Qubits er laget av fysiske ting, og vi trenger andre fysiske ting i nærheten for å kontrollere og måle dem. Qubits er «dumme», og de vil koble seg til alt de kan. Vi må designe qubitene svært nøye for å beskytte dem fra å koble seg til omgivelsene.
- Støy: Vi må beskytte qubitene våre mot alle typer støy, som kosmisk stråling, stråling, varmeenergi eller uønskede partikler. En viss grad av dekoherens og støy er uunngåelig i ethvert fysisk system og er umulig å eliminere fullstendig.
- Skalerbarhet: For hver qubit trenger vi en haug med ledninger for å manipulere og måle den. Etter hvert som vi legger til flere qubits, vokser den nødvendige infrastrukturen lineært, noe som utgjør en betydelig ingeniørutfordring. Ethvert design på en kvantedatamaskin må finne en måte å effektivt koble sammen, kontrollere og måle alle disse qubitene på mens systemet skaleres opp.
- Kvantefeilkorreksjon: Kvantefeilkorreksjon er et feilkorrigeringssystem som brukes til å lage feiltolerante kvantedatamaskiner. Dette gjøres ved å bruke mange sammenfiltrede qubits til å representere én støyfri qubit. Det krever et stort antall fysiske qubits for å lage én feiltolerant qubit.
Fysiske implementeringer

Det finnes mange ulike fysiske implementeringer av kvantedatamaskiner, ettersom det finnes mange ulike kvantesystemer de kan bygges av. Her er noen av de mest brukte og vellykkede tilnærmingene:
- Superledende kvantedatamaskiner: Superledende qubits er for tiden den mest populære tilnærmingen. Disse qubitene er laget av superledende ledninger med et brudd i superlederen kalt en Josephson-overgang. Den mest populære typen superledende qubit kalles en transmon.
- Kvantepunkt kvantedatamaskiner: Qubits lages av elektroner eller grupper av elektroner, og to-nivåsystemet kodes inn i spinn eller ladningen til elektronene. Disse qubitene er bygget av halvledere som silisium.
- Lineær optisk kvanteberegning: Optiske kvantedatamaskiner bruker lysfotoner som qubits og opererer på disse ved hjelp av optiske elementer som speil, bølgeplater og interferometre.
- Fanget ion kvantedatamaskiner: Ladede atomer brukes som qubits. Disse atomene er ioniserte og mangler et elektron. To-nivåtilstanden som koder for qubit, er de spesifikke energinivåene til atomet, som kan manipuleres eller måles med mikrobølger eller laserstråler.
- Fargesenter eller Nitrogen Vacancy kvantedatamaskiner: Disse qubitene er laget av atomer som er innebygd i materialer som nitrogen i diamant eller silisiumkarbid. De skapes ved hjelp av kjernefysiske spinn av de innebygde atomene og er koblet sammen med elektroner.
- Nøytrale atomer i optiske gitre: Denne tilnærmingen fanger nøytrale atomer inn i et optisk gitter, som er et kryssarrangement av laserstråler. To-nivåsystemet for qubitene kan være det hyperfine energinivået til atomet eller de eksiterte tilstandene.
Dette er noen av de viktigste tilnærmingene til å bygge kvantedatamaskiner, hver med sine egne unike egenskaper og utfordringer. Kvanteberegning er i rask endring, og det å velge riktig tilnærming er avgjørende for fremtidig suksess.
Bruksområder for kvantedatamaskiner

- Kvantesimulering: Kvantedatamaskiner har potensiale til å simulere komplekse kvantesystemer, slik at vi kan studere kjemiske reaksjoner, elektronenes oppførsel i materialer og ulike fysiske parametere. Dette kan brukes til å forbedre solcellepaneler, batterier, medikamentutvikling, romfartsmaterialer og mye mer.
- Kvantealgoritmer: Algoritmer som Shors algoritme og Grovers algoritme kan løse problemer som anses som vanskelige for klassiske datamaskiner. Disse har applikasjoner innen kryptografi, optimalisering av komplekse systemer, maskinlæring og kunstig intelligens.
- Cybersikkerhet: Kvantedatamaskiner utgjør en trussel mot klassiske krypteringssystemer. Men de kan også bidra til cybersikkerhet gjennom utvikling av kvantebestandige krypteringssystemer. Kvantekryptografi, som er relatert til kvanteberegning, kan også forbedre sikkerheten.
- Optimaliseringsproblemer: Kvantedatamaskiner kan takle komplekse optimaliseringsproblemer mer effektivt enn klassiske datamaskiner. Dette kan brukes i ulike bransjer, fra logistikk til finansmodeller.
- Værvarsling og klimaendringer: Selv om det ikke er grundig forklart i artikkelen, kan kvantedatamaskiner forbedre værvarslingsmodeller og bidra til å løse klimarelaterte utfordringer. Dette er et område som kan dra nytte av kvanteberegning i fremtiden.
- Kvantekryptografi: Kvantekryptografi øker datasikkerheten ved å bruke kvanteprinsipper for sikker kommunikasjon. I en tid med økende cybertrusler er dette svært viktig.
Vi må imidlertid være litt forsiktige med hypen som er bygget opp rundt denne teknologien. Mange av påstandene om hva kvantedatamaskiner vil være gode for kommer fra aktører som aktivt samler inn penger til å bygge dem.
Mitt syn er at historisk sett, når en ny teknologi har dukket opp, har ikke datidens mennesker vært de beste til å forutse hva den skal brukes til.
For eksempel drømte ikke de som oppfant de første datamaskinene om internett og alt det innebærer. Sannsynligvis vil det samme gjelde for kvantedatamaskiner.
Avsluttende tanker
Kvantedatamaskiner blir stadig bedre, og selv om vi ikke kan bruke dem i hverdagen ennå, har de potensial for mange praktiske bruksområder i fremtiden.
I denne artikkelen har vi diskutert ulike aspekter ved kvantedatamaskiner, inkludert de grunnleggende konseptene superposisjon, sammenfiltring og interferens.
Deretter utforsket vi kvantealgoritmer, inkludert Shors algoritme og Grovers algoritme. Vi fordypet oss også i kvantekompleksitetsteori og de ulike modellene for kvantedatamaskiner.
Vi har også sett på utfordringene og praktiske spørsmål knyttet til kvanteberegning. Til slutt har vi sett på det brede spekteret av potensielle bruksområder for kvantedatamaskiner.
Du kan også lese om vanlige spørsmål om kvanteberegning.