Big O-analyse er en metode for å vurdere og sammenligne effektiviteten til ulike algoritmer.
Dette gjør det lettere å velge algoritmer som er mest effektive og kan håndtere store datamengder. Denne artikkelen fungerer som en Big O jukseguide, og forklarer alt du bør vite om Big O-notasjon.
Hva er Big O-analyse?
Big O-analyse er en teknikk som brukes for å analysere hvor godt en algoritme presterer når datamengden øker. Vi undersøker spesielt hvor effektiv algoritmen er når størrelsen på inndataene vokser.
Med effektivitet menes hvor godt systemressurser blir brukt for å produsere et resultat. De ressursene vi er mest opptatt av, er tid og minne.
Når vi utfører Big O-analyse, stiller vi oss derfor følgende spørsmål:
- Hvordan endres minnebruken til en algoritme når inndatastørrelsen øker?
- Hvordan endres tiden det tar for en algoritme å produsere et resultat, når inndatastørrelsen øker?
Svaret på det første spørsmålet gir algoritmens romkompleksitet, mens svaret på det andre spørsmålet gir tidskompleksiteten. Vi benytter en spesiell notasjon som kalles Big O-notasjon for å uttrykke svarene på begge spørsmålene. Dette vil bli forklart nærmere i denne Big O-jukseguiden.
Forutsetninger
Før vi går videre, er det viktig å nevne at for å få mest mulig ut av denne Big O-jukseguiden, bør du ha en grunnleggende forståelse for algebra. I tillegg, siden vi vil bruke eksempler i Python, er det også fordelaktig å ha litt kjennskap til Python. En dyptgående forståelse er ikke nødvendig, da du ikke skal skrive kode selv.
Hvordan utføre Big O-analyse
I dette avsnittet skal vi se nærmere på hvordan man utfører Big O-analyse.
Når man analyserer kompleksiteten ved hjelp av Big O, er det viktig å huske at algoritmens ytelse avhenger av hvordan inndataene er organisert.
For eksempel vil sorteringsalgoritmer fungere raskest når dataene i en liste allerede er sortert i riktig rekkefølge. Dette er det beste scenariet for algoritmens ytelse. På den andre siden vil de samme sorteringsalgoritmene være tregest når dataene er organisert i omvendt rekkefølge. Dette er det verste scenariet.
Når vi utfører Big O-analyse, tar vi kun hensyn til det verste scenarioet.
Romkompleksitetsanalyse

La oss begynne denne Big O-jukseguiden med å se på hvordan man utfører en romkompleksitetsanalyse. Vi vil vurdere hvordan det ekstra minnet som en algoritme bruker, endrer seg når inndataene blir større og større.
For eksempel bruker funksjonen nedenfor rekursjon for å telle ned fra n til null. Den har en romkompleksitet som er direkte proporsjonal med n. Dette er fordi når n vokser, øker også antall funksjonskall på anropsstakken. Dermed har den en romkompleksitet på O(n).
def loop_recursively(n):
if n == -1:
return
else:
print(n)
loop_recursively(n - 1)
En mer effektiv implementering kan se slik ut:
def loop_normally(n):
count = n
while count >= 0:
print(count)
count =- 1
I algoritmen over lager vi bare én ekstra variabel og bruker den til å utføre en løkke. Selv om n skulle bli større og større, ville vi fortsatt bare bruke én ekstra variabel. Derfor har denne algoritmen en konstant romkompleksitet, som betegnes med symbolet «O(1)».
Ved å sammenligne romkompleksiteten til de to algoritmene, kan vi konkludere med at while-løkken er mer effektiv enn rekursjon. Dette er hovedpoenget med Big O-analyse: å analysere hvordan algoritmer oppfører seg når vi bruker større inndata.
Tidskompleksitetsanalyse

Når vi utfører tidskompleksitetsanalyse, er vi ikke opptatt av den totale tiden algoritmen bruker, men derimot økningen i antall beregningstrinn. Dette er fordi den faktiske tiden avhenger av mange systemmessige og tilfeldige faktorer som er vanskelig å ta hensyn til. Derfor ser vi kun på økningen i beregningstrinn og antar at hvert trinn tar like lang tid.
For å demonstrere tidskompleksitetsanalyse, la oss se på følgende eksempel:
Anta at vi har en liste med brukere, der hver bruker har en ID og et navn. Vår oppgave er å implementere en funksjon som returnerer brukerens navn når vi oppgir en ID. Her er en måte å gjøre det på:
users = [
{'id': 0, 'name': 'Alice'},
{'id': 1, 'name': 'Bob'},
{'id': 2, 'name': 'Charlie'},
]
def get_username(id, users):
for user in users:
if user['id'] == id:
return user['name']
return 'User not found'
get_username(1, users)
Gitt en liste over brukere, går algoritmen vår gjennom hele brukerlisten for å finne brukeren med riktig ID. Hvis vi har 3 brukere, utfører algoritmen 3 iterasjoner. Hvis vi har 10 brukere, utfører den 10 iterasjoner.
Dermed er antall trinn lineært og direkte proporsjonalt med antall brukere. Algoritmen vår har derfor en lineær tidskompleksitet. Men vi kan forbedre algoritmen vår.
Anta at i stedet for å lagre brukerne i en liste, lagret vi dem i en ordbok. Da vil algoritmen vår for å finne en bruker se slik ut:
users = {
'0': 'Alice',
'1': 'Bob',
'2': 'Charlie'
}
def get_username(id, users):
if id in users:
return users[id]
else:
return 'User not found'
get_username(1, users)
Med denne nye algoritmen, la oss si at vi har 3 brukere i ordboken. Vi ville ha utført et visst antall trinn for å finne brukernavnet. Og la oss si at vi har flere brukere, for eksempel ti. Vi ville ha utført det samme antall trinn som før for å finne brukeren. Etter hvert som antall brukere øker, forblir antall trinn for å finne et brukernavn konstant.
Derfor har denne nye algoritmen en konstant kompleksitet. Det spiller ingen rolle hvor mange brukere vi har, antall beregningstrinn er det samme.
Hva er Big O-notasjon?
I forrige avsnitt diskuterte vi hvordan man beregner Big O rom- og tidskompleksitet for ulike algoritmer. Vi brukte ord som lineær og konstant for å beskrive kompleksiteten. En annen måte å beskrive kompleksiteten på, er ved hjelp av Big O-notasjon.
Big O-notasjon er en måte å representere en algoritmes rom- eller tidskompleksitet på. Notasjonen er ganske enkel, det er en O etterfulgt av parenteser. Inni parentesene skriver vi en funksjon av n for å representere den spesielle kompleksiteten.
Lineær kompleksitet representeres av n, så vi skriver den som O(n) (leses som «O av n»). Konstant kompleksitet representeres av 1, så vi skriver den som O(1).
Det finnes flere typer kompleksitet, som vi vil diskutere i neste avsnitt. Generelt, for å skrive en algoritmes kompleksitet, følger du disse trinnene:
- Prøv å utvikle en matematisk funksjon av n, f(n), der f(n) er mengden plass som brukes eller antall beregningstrinn algoritmen utfører, og n er inndatastørrelsen.
- Velg det mest dominerende leddet i funksjonen. Rekkefølgen av dominans for ulike ledd, fra mest til minst dominant, er som følger: Fakultet, Eksponentiell, Polynomisk, Kvadratisk, Linearitermisk, Lineær, Logaritmisk og Konstant.
- Fjern eventuelle koeffisienter fra leddet.
Resultatet av dette blir leddet vi bruker inni parentesene.
Eksempel:
La oss se på følgende Python-funksjon:
users = [
'Alice',
'Bob',
'Charlie'
]
def print_users(users):
number_of_users = len(users)
print("Total number of users:", number_of_users)
for i in number_of_users:
print(i, end=': ')
print(user)
Nå skal vi beregne algoritmens Big O-tidskompleksitet.
Først skriver vi en matematisk funksjon av n, f(n), for å representere antall beregningstrinn algoritmen tar. Husk at n representerer inndatastørrelsen.
Ut fra koden vår utfører funksjonen to trinn: ett for å beregne antall brukere, og et annet for å skrive ut det totale antallet brukere. Deretter, for hver bruker, utfører den to trinn: ett for å skrive ut indeksen og ett for å skrive ut brukeren.
Funksjonen som best representerer antall beregningstrinn, kan dermed skrives som f(n) = 2 + 2n, der n er antall brukere.
Vi går videre til trinn to og velger det mest dominerende leddet. 2n er et lineært ledd, og 2 er et konstant ledd. Lineært er mer dominant enn konstant, så vi velger 2n, det lineære leddet.
Nå har vi funksjonen f(n) = 2n.
Det siste trinnet er å fjerne koeffisientene. I funksjonen vår har vi 2 som koeffisient. Så vi fjerner den. Funksjonen blir dermed f(n) = n. Dette er leddet vi bruker inni parentesene.
Derfor er tidskompleksiteten til algoritmen vår O(n), eller lineær kompleksitet.
Ulike Big O-kompleksiteter
Siste delen av vår Big O-jukseguide vil vise deg de ulike kompleksitetene og de tilhørende grafene.
#1. Konstant

Konstant kompleksitet betyr at algoritmen bruker en konstant mengde plass (når vi utfører en romkompleksitetsanalyse) eller et konstant antall trinn (når vi utfører en tidskompleksitetsanalyse). Dette er den mest optimale kompleksiteten, siden algoritmen ikke krever ekstra plass eller tid når inndataene vokser. Den er derfor svært skalerbar.
Konstant kompleksitet representeres som O(1). Det er imidlertid ikke alltid mulig å lage algoritmer som kjører med konstant kompleksitet.
#2. Logaritmisk
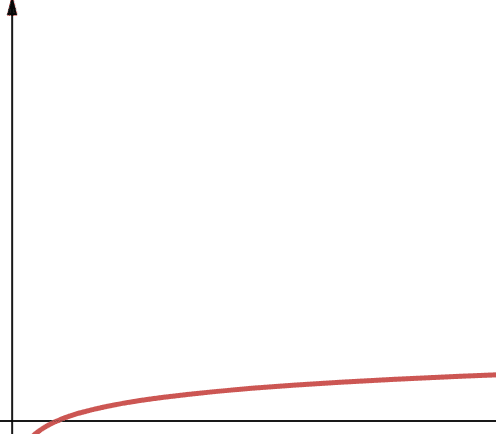
Logaritmisk kompleksitet representeres av leddet O(log n). Det er viktig å merke seg at hvis logaritmens basis ikke er spesifisert i informatikk, antar vi at den er 2.
Derfor er log n det samme som log2n. Logaritmiske funksjoner er kjent for å vokse raskt i starten, og deretter sakke ned. Dette betyr at de er skalerbare og fungerer effektivt med stadig større verdier for n.
#3. Lineær
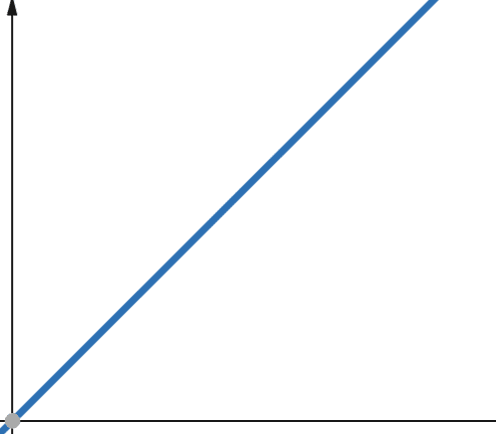
For lineære funksjoner gjelder det at hvis den uavhengige variabelen skaleres med en faktor p, så skaleres den avhengige variabelen med samme faktor p.
Dermed vil en funksjon med en lineær kompleksitet vokse med samme faktor som inndatastørrelsen. Hvis inndatastørrelsen dobles, vil antall beregningstrinn eller minnebruk også dobles. Lineær kompleksitet representeres med symbolet O(n).
#4. Linearitermisk
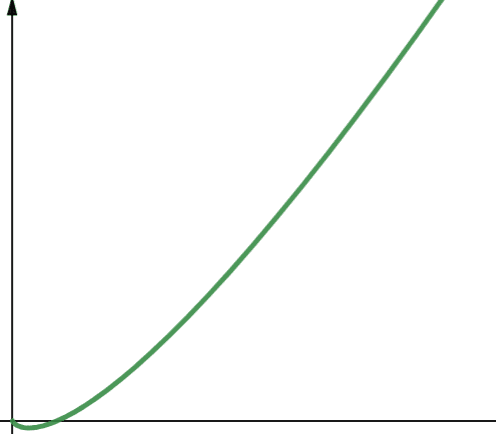
O(n * log n) representerer linearitermiske funksjoner. Linearitermiske funksjoner er en lineær funksjon multiplisert med en logaritmisk funksjon. En linearitermisk funksjon gir dermed resultater som er litt større enn lineære funksjoner når log n er større enn 1. Dette er fordi n øker når det multipliseres med et tall større enn 1.
Log n er større enn 1 for alle verdier av n større enn 2 (husk at log n er log2n). Derfor er linearitermiske funksjoner mindre skalerbare enn lineære funksjoner for alle verdier av n som er større enn 2. I de fleste tilfeller er n større enn 2. Dermed er linearitermiske funksjoner generelt mindre skalerbare enn logaritmiske funksjoner.
#5. Kvadratisk
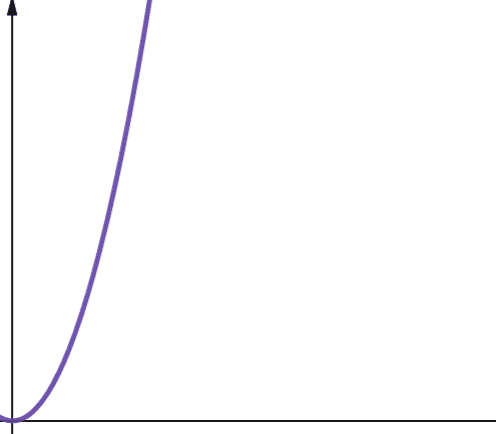
Kvadratisk kompleksitet representeres med O(n²). Dette betyr at hvis inndatastørrelsen din øker med 10 ganger, øker antall trinn som tas eller plass som brukes, med 10² ganger, eller 100! Dette er ikke særlig skalerbart, og som du ser på grafen, øker kompleksiteten veldig raskt.
Kvadratisk kompleksitet oppstår i algoritmer der du går gjennom en løkke n ganger, og for hver iterasjon går gjennom en løkke n ganger til, for eksempel i Bubble Sort. Selv om det generelt ikke er ideelt, har du noen ganger ikke noe annet valg enn å implementere algoritmer med kvadratisk kompleksitet.
#6. Polynom
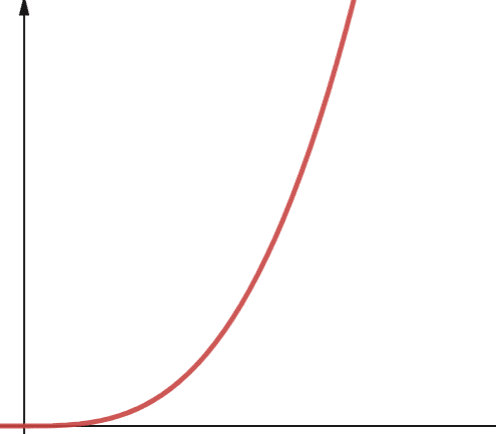
En algoritme med polynomisk kompleksitet representeres med O(np), der p er et konstant heltall. p representerer potensen som n heves til.
Denne kompleksiteten oppstår når du har flere nestede løkker. Forskjellen mellom polynomisk og kvadratisk kompleksitet er at kvadratisk kompleksitet har en orden på 2, mens polynomisk kompleksitet har et hvilket som helst tall større enn 2.
#7. Eksponentiell
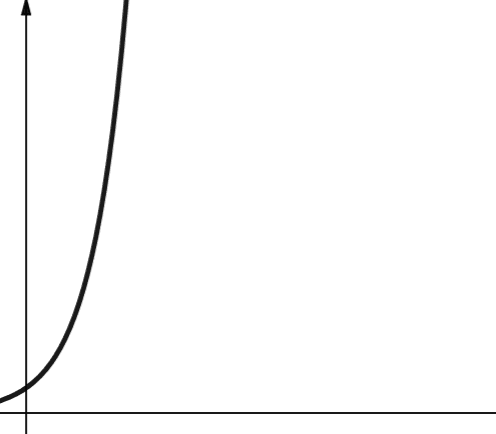
Eksponentiell kompleksitet vokser enda raskere enn polynomisk kompleksitet. I matematikken er standardverdien for eksponentialfunksjonen konstanten e (Eulers tall). I informatikk er imidlertid standardverdien for eksponentialfunksjonen 2.
Eksponentiell kompleksitet representeres med symbolet O(2n). Når n er 0, er 2n lik 1. Men når n øker til 5, øker 2n til 32. En økning i n med én vil doble det forrige tallet. Derfor er funksjoner av eksponentiell karakter ikke særlig skalerbare.
#8. Fakultet
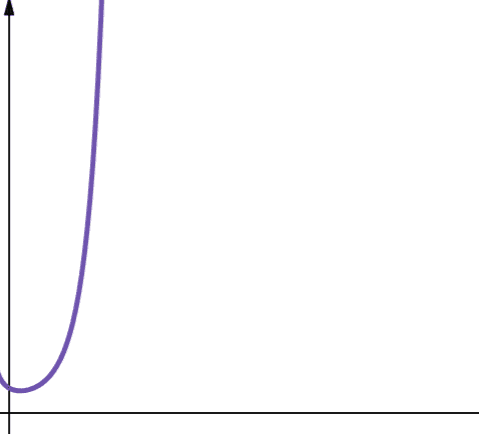
Fakultetskompleksitet representeres med symbolet O(n!). Denne funksjonen vokser også veldig raskt og er dermed ikke skalerbar.
Konklusjon
Denne artikkelen har omhandlet Big O-analyse og hvordan du beregner den. Vi har også diskutert de ulike kompleksitetene og deres skalerbarhet.
Du kan nå prøve å øve på Big O-analyse ved å se på Python-sorteringsalgoritmer.