Excel tilbyr innebygde funksjoner som gjør det mulig å visualisere kalibreringsdata og beregne den best passende linjen. Dette er spesielt nyttig når du skal utarbeide en kjemirapport for laboratoriet eller programmere en korreksjonsfaktor i et utstyr.
I denne artikkelen skal vi utforske hvordan du kan bruke Excel til å generere et diagram, plotte en lineær kalibreringskurve, presentere kalibreringskurvens formel, og deretter sette opp enkle formler med funksjonene STIGNING og SKJÆRINGSPUNKT for å anvende kalibreringsligningen i Excel.
Hva er en kalibreringskurve og hvordan forenkler Excel prosessen?
En kalibrering innebærer å sammenligne målinger fra en enhet (for eksempel temperaturen som vises på et termometer) med kjente referanseverdier, også kalt standarder (som fryse- og kokepunktene for vann). Dette gir deg en samling av datapunkter som danner grunnlaget for en kalibreringskurve.
En topunktskalibrering av et termometer ved bruk av vannets fryse- og kokepunkter resulterer i to datapunkter: ett fra termometeret i isvann (0°C) og ett fra kokende vann (100°C). Når disse datapunktene plottes i et diagram og en linje trekkes mellom dem (kalibreringskurven), forutsatt at termometerets respons er lineær, kan du bruke denne linjen til å finne den «sanne» temperaturen for alle punkter langs linjen, basert på hva termometeret viser.
Dermed fyller linjen ut informasjonen mellom de to kjente punktene, noe som gir deg en rimelig nøyaktig estimering av den faktiske temperaturen når termometeret viser 57,2 grader, selv om du ikke har målt en «standard» som tilsvarer den spesifikke avlesningen.
Excel tilbyr verktøy for å grafisk fremstille datapunktene i et diagram, legge til en trendlinje (kalibreringskurven) og vise kalibreringskurvens ligning direkte i diagrammet. Dette gir ikke bare en visuell presentasjon, men du kan også beregne linjens formel ved hjelp av Excels STIGNING- og SKJÆRINGSPUNKT-funksjoner. Når disse verdiene integreres i enkle formler, kan du automatisk beregne den «sanne» verdien for enhver måling.
La oss se på et praktisk eksempel
I dette eksemplet skal vi utvikle en kalibreringskurve basert på ti datapunkter, hver bestående av en X-verdi og en Y-verdi. X-verdiene vil representere våre «standarder», og kan være alt fra konsentrasjonen av en kjemisk løsning målt med et vitenskapelig instrument, til inngangsvariabelen i et program som styrer en maskin.
Y-verdiene vil representere «svarene», og kan være avlesningen fra instrumentet ved måling av hver kjemisk løsning, eller den målte avstanden fra utskytningsrampen til der en kule lander, for hver inngangsverdi.
Etter å ha grafisk representert kalibreringskurven, vil vi bruke STIGNING- og SKJÆRINGSPUNKT-funksjonene for å beregne formelen for kalibreringslinjen. Dette vil hjelpe oss med å bestemme konsentrasjonen av en «ukjent» kjemisk løsning basert på instrumentets måling, eller finne den korrekte inngangsverdien for å få en kule til å lande en bestemt distanse fra utskyteren.
Trinn 1: Lag diagrammet
Vårt enkle regneark består av to kolonner: X-verdi og Y-verdi.
La oss starte med å velge dataene som skal plottes i diagrammet.
Først velger du cellene i «X-verdi»-kolonnen.
Hold Ctrl-tasten nede og klikk deretter på cellene i «Y-verdi»-kolonnen.
Gå til «Sett inn»-fanen.

Naviger til «Diagrammer»-menyen og velg det første alternativet i «Punkt»-rullegardinmenyen.
Et diagram som inneholder punktene fra de to kolonnene vil nå vises.
Velg serien ved å klikke på et av de blå punktene. Excel vil markere punktene som er en del av serien.
Høyreklikk på et av punktene og velg deretter «Legg til trendlinje».
En rett linje vil nå vises i diagrammet.
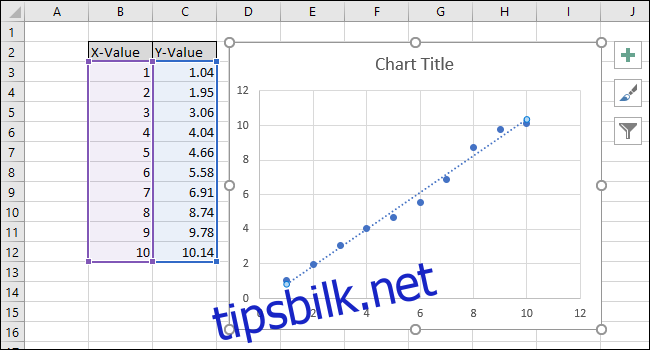
På høyre side av skjermen vil menyen «Formater trendlinje» vises. Kryss av boksene for «Vis ligning i diagrammet» og «Vis R-kvadratverdi i diagrammet». R-kvadratverdien indikerer hvor godt linjen tilpasser seg dataene. En R-kvadratverdi på 1.000 er ideell, og betyr at alle punktene ligger direkte på linjen. Lavere R-kvadratverdier indikerer større avstand mellom punktene og linjen, med 0.000 som laveste verdi.
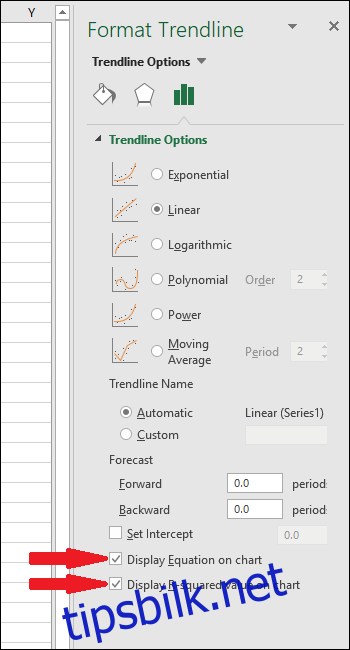
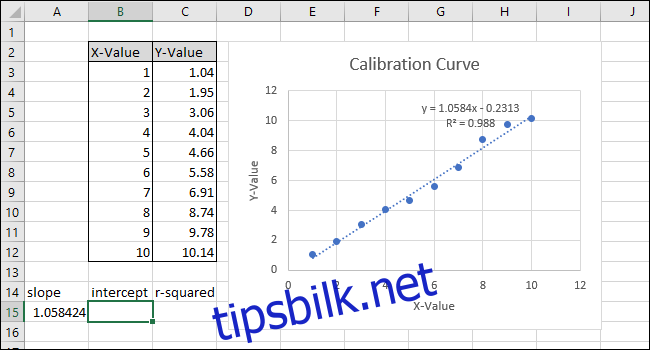
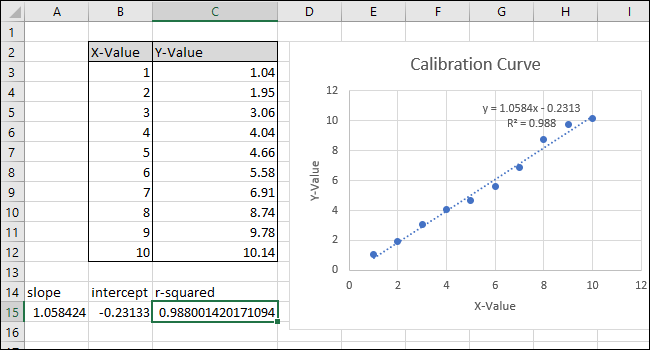
Ligningen og R-kvadratverdien vil nå vises i diagrammet. I vårt eksempel ser vi at korrelasjonen er veldig god, med en R-kvadratverdi på 0.988.
Ligningen har formen «Y = Mx + B», der M er stigningen og B er skjæringspunktet med y-aksen.
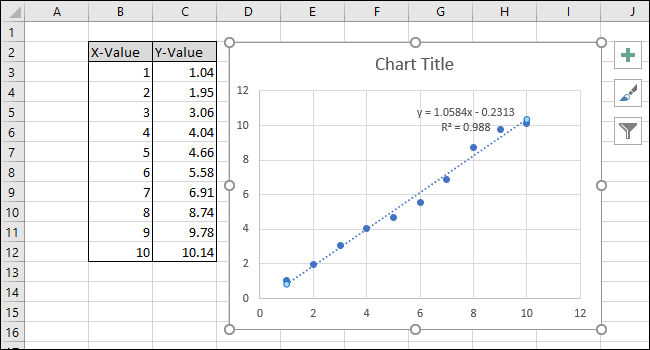
Nå som kalibreringen er fullført, kan vi forbedre diagrammet ved å endre tittelen og legge til aksetitler.
For å endre diagramtittelen, klikk på den for å velge teksten.
Skriv inn en ny tittel som beskriver diagrammet.
For å legge til titler til x-aksen og y-aksen, gå først til «Diagramverktøy > Design».
Klikk på rullegardinmenyen «Legg til diagramelement».
Naviger nå til «Aksetitler > Primær horisontal».
En aksetittel vil nå vises.
For å gi nytt navn til aksens tittel, velg teksten og skriv deretter inn en ny tittel.
Gå deretter til «Aksetitler > Primær vertikal».
En aksetittel vil nå vises.
Gi denne tittelen et nytt navn ved å velge teksten og skrive inn en ny tittel.
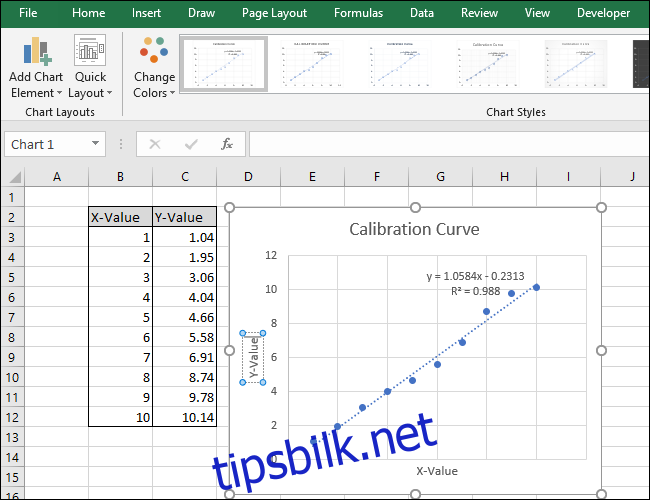
Diagrammet ditt er nå ferdig.
Trinn 2: Beregn linjeligningen og R-kvadratverdien
La oss nå beregne linjeligningen og R-kvadratverdien ved hjelp av Excels innebygde funksjoner STIGNING, SKJÆRINGSPUNKT og KORRELASJON.
Vi har lagt til titler for disse tre funksjonene i regnearket vårt (i rad 14). De faktiske beregningene vil bli utført i cellene under disse titlene.
Først skal vi beregne STIGNINGEN. Velg celle A15.
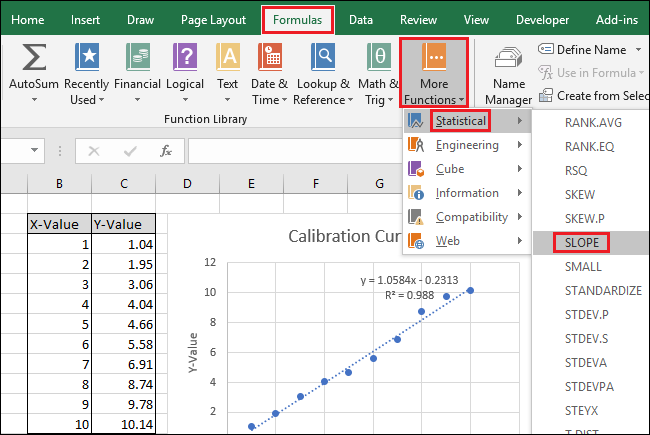
Naviger til «Formler > Flere funksjoner > Statistikk > STIGNING».
Funksjonsargumentvinduet vil nå vises. I feltet «Kjente_y-verdier» velger du eller skriver inn cellene i Y-verdi-kolonnen.
I feltet «Kjente_x-verdier» velger du eller skriver inn cellene i X-verdi-kolonnen. Rekkefølgen på feltene «Kjente_y-verdier» og «Kjente_x-verdier» er avgjørende i STIGNING-funksjonen.
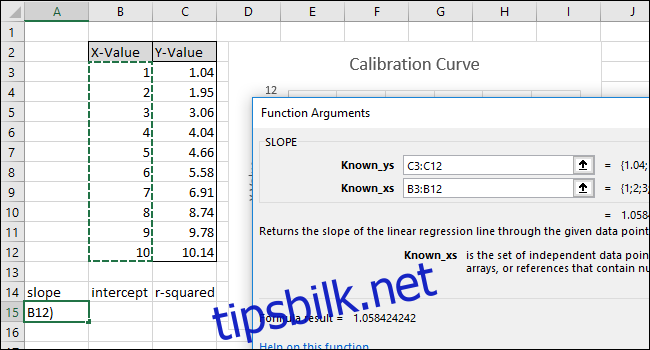
Klikk «OK». Den endelige formelen i formellinjen skal se slik ut:
=STIGNING(C3:C12;B3:B12)
Legg merke til at verdien som returneres av STIGNING-funksjonen i celle A15 stemmer overens med verdien som vises i diagrammet.
Velg deretter celle B15 og naviger til «Formler > Flere funksjoner > Statistisk > SKJÆRINGSPUNKT».
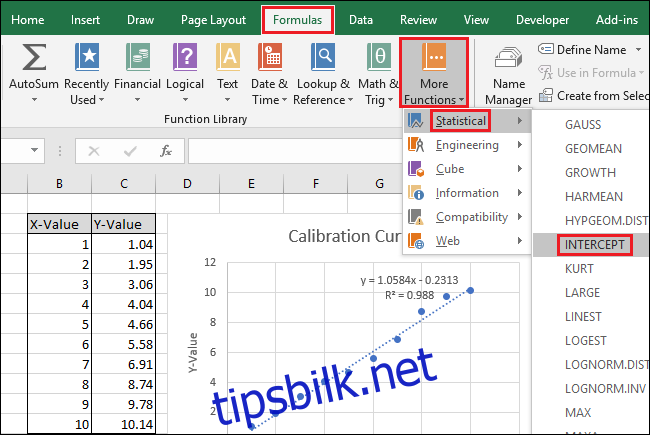
Funksjonsargumentvinduet vil nå vises. Velg eller skriv inn cellene i Y-verdi-kolonnen for feltet «Kjente_y-verdier».
Velg eller skriv inn cellene i X-verdi-kolonnen for feltet «Kjente_x-verdier». Rekkefølgen på feltene «Kjente_y-verdier» og «Kjente_x-verdier» er også avgjørende for SKJÆRINGSPUNKT-funksjonen.
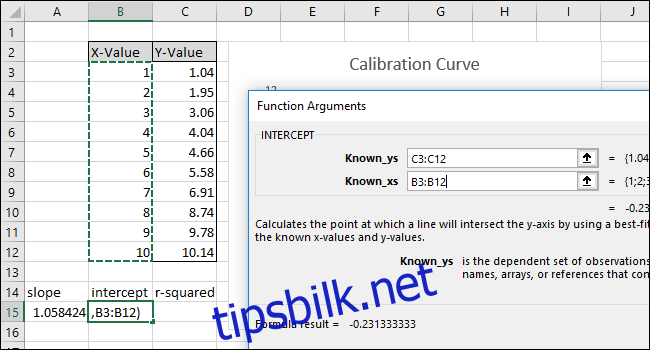
Klikk «OK». Den endelige formelen i formellinjen skal se slik ut:
=SKJÆRING(C3:C12;B3:B12)
Legg merke til at verdien som returneres av SKJÆRINGSPUNKT-funksjonen stemmer overens med y-skjæringspunktet som vises i diagrammet.
Velg deretter celle C15 og naviger til «Formler > Flere funksjoner > Statistisk > KORRELASJON».
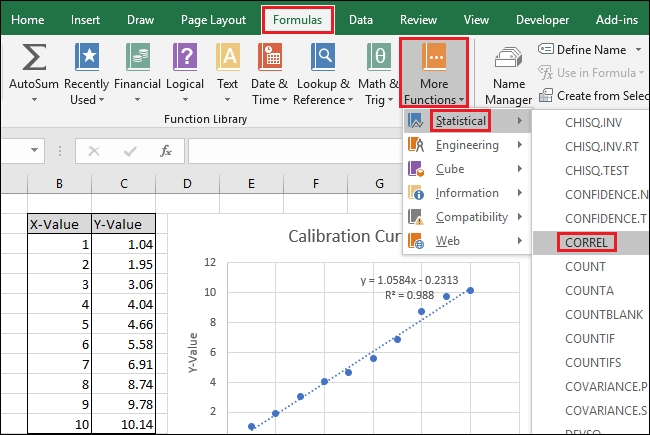
Funksjonsargumentvinduet vil nå vises. Velg eller skriv inn et av de to celleområdene for feltet «Matrise1». I motsetning til STIGNING og SKJÆRINGSPUNKT, påvirker ikke rekkefølgen resultatet av KORRELASJON-funksjonen.
Velg eller skriv inn det andre av de to celleområdene for feltet «Matrise2».
Klikk «OK». Formelen skal se slik ut i formellinjen:
=KORREL(B3:B12;C3:C12)
Legg merke til at verdien som returneres av KORRELASJON-funksjonen ikke stemmer overens med R-kvadratverdien i diagrammet. KORRELASJON-funksjonen returnerer «R», så vi må kvadrere den for å beregne «R-kvadrert».
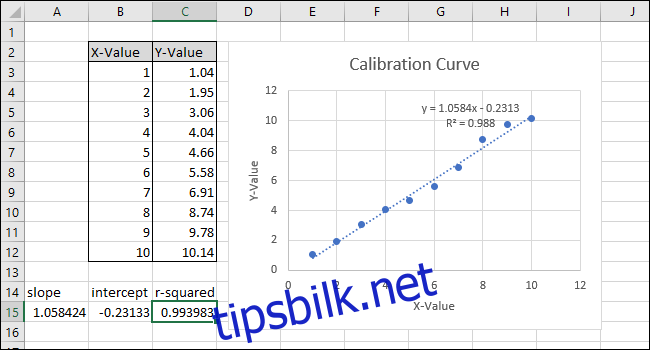
Klikk inne i formellinjen og legg til «^2» på slutten av formelen for å kvadrere verdien som returneres av KORRELASJON-funksjonen. Den fullførte formelen skal nå se slik ut:
=KORREL(B3:B12;C3:C12)^2
Trykk Enter.
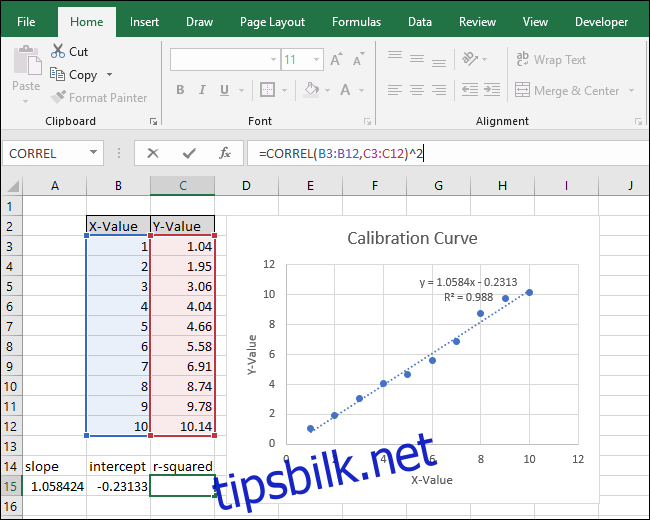
Etter å ha endret formelen stemmer nå R-kvadratverdien overens med den som vises i diagrammet.
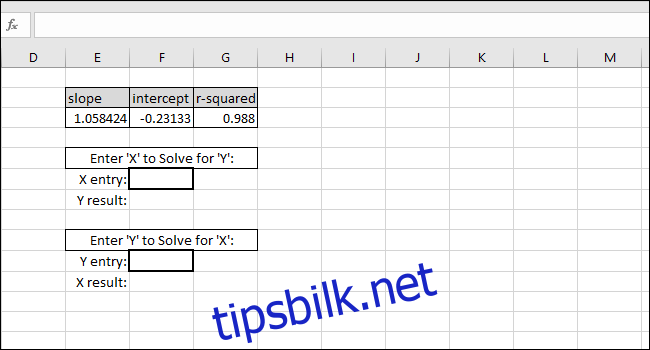
Trinn 3: Sett opp formler for rask beregning av verdier
Nå kan vi bruke disse verdiene i enkle formler for å bestemme konsentrasjonen av den «ukjente» løsningen eller finne den inngangsverdien vi skal bruke i koden for at kulen skal fly en bestemt avstand.
Disse trinnene vil sette opp formlene som kreves for at du kan legge inn en X-verdi eller en Y-verdi og få den tilsvarende verdien basert på kalibreringskurven.
Ligningen for den best passende linjen er i formen «Y-verdi = STIGNING * X-verdi + SKJÆRINGSPUNKT», så for å løse for «Y-verdien» multipliseres X-verdien med STIGNING og deretter legges SKJÆRINGSPUNKT til.
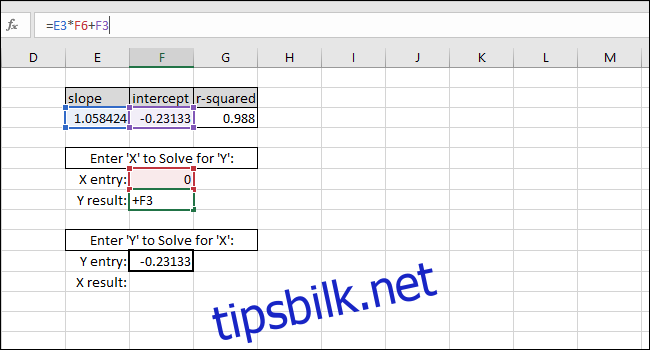
Som et eksempel setter vi null som X-verdi. Y-verdien som returneres skal være lik SKJÆRINGSPUNKTET for den best passende linjen. Det stemmer, så vi vet at formelen fungerer som den skal.
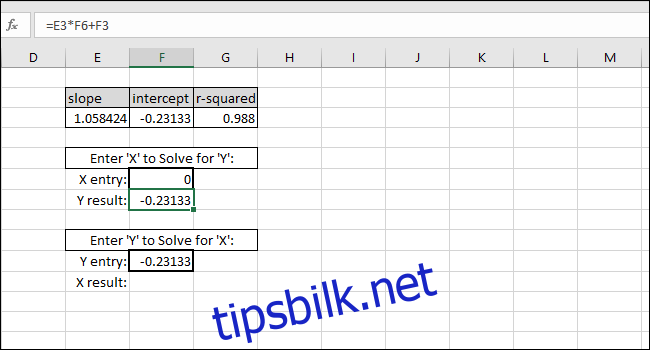
Å løse for X-verdien basert på en Y-verdi gjøres ved å trekke SKJÆRINGSPUNKTET fra Y-verdien og dele resultatet på STIGNING:
X-verdi=(Y-verdi-SKJÆRINGSPUNKT)/STIGNING
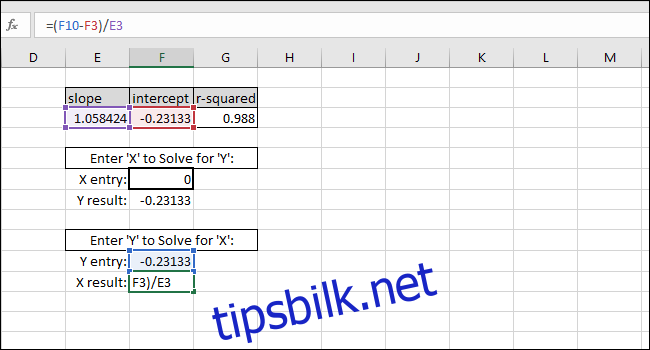
Som et eksempel brukte vi SKJÆRINGSPUNKTET som en Y-verdi. X-verdien som returneres skal være lik null, men verdien som returneres er 3.14934E-06. Verdien som returneres er ikke null fordi vi utilsiktet avkortet SKJÆRINGSPUNKT-resultatet da vi skrev inn verdien. Formelen fungerer imidlertid, ettersom resultatet av formelen er 0.00000314934, som i bunn og grunn er null.
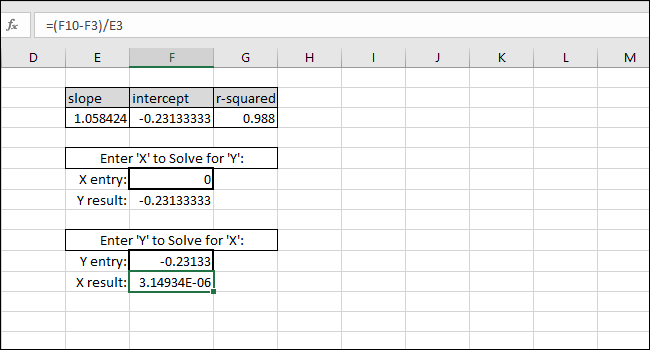
Du kan legge inn hvilken som helst X-verdi du ønsker i den første cellen med tykke kanter, og Excel vil automatisk beregne den tilsvarende Y-verdien.
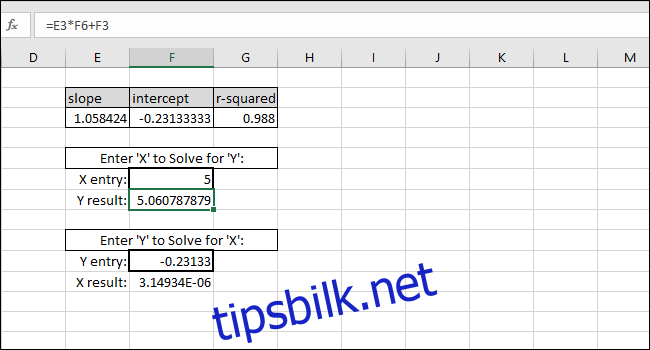
Hvis du legger inn en hvilken som helst Y-verdi i den andre cellen med tykke kanter, vil du få den tilsvarende X-verdien. Denne formelen er det du vil bruke til å beregne konsentrasjonen av løsningen eller hvilken inngangsverdi som trengs for å skyte kulen en bestemt avstand.
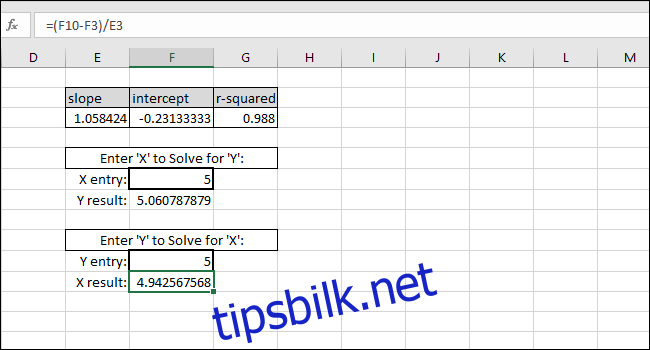
I dette tilfellet viser instrumentet «5», så kalibreringen antyder en konsentrasjon på 4.94. Alternativt, hvis vi vil at kulen skal reise fem lengdeenheter, indikerer kalibreringen at vi skal legge inn 4.94 som inngangsvariabel for programmet som styrer kulens utskyting. Vi kan ha rimelig tiltro til disse resultatene på grunn av den høye R-kvadratverdien i dette eksemplet.