Sortering er en fundamental operasjon innen programmering, og valget av algoritme er avgjørende for å oppnå effektivitet. Feil algoritme kan føre til betydelig tidsbruk, spesielt ved behandling av store datamengder.
I denne artikkelen vil vi utforske et utvalg av sorteringsalgoritmer, og vi vil presentere dem på en måte som gjør det enkelt å forstå implementeringen.
Vi går gjennom ulike sorteringsalgoritmer, trinn for trinn, med Python som implementeringsspråk. Når du forstår den underliggende logikken, kan du enkelt overføre den til ethvert annet programmeringsspråk. Det handler mest om språksyntaks.
I denne gjennomgangen vil vi gradvis bevege oss fra de minst effektive til de mest effektive algoritmene. Så heng med, studer algoritmene og prøv dem ut selv.
La oss starte vår reise inn i sorteringsalgoritmenes verden.
Innsettingssortering
Innsettingssortering er en av de enkleste sorteringsalgoritmene å forstå og implementere. Likevel er den ikke den mest effektive for store datamengder, da den kan være tidkrevende. Derfor brukes den sjeldnere i praktiske tilfeller med betydelige datamengder.
Innsettingssorteringsalgoritmen deler det gitte arrayet i en sortert og en usortert del.
Den sorterte delen begynner med kun det første elementet. Vi tar deretter elementer fra den usorterte delen og plasserer dem på riktig sted i den sorterte delen.
La oss illustrere prosessen trinn for trinn med et eksempel.
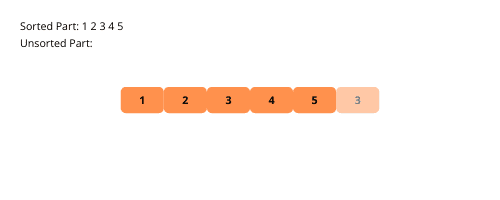
Fremgangsmåten for å implementere innsettingssortering er som følger:
- Initialiser arrayet med testdata (heltall).
- Gå gjennom arrayet fra og med det andre elementet.
- Lagre gjeldende posisjon og element i separate variabler.
- Start en løkke som går bakover gjennom arrayet frem til det første elementet eller et element som er mindre enn det gjeldende elementet.
- Flytt det forrige elementet fremover (erstatt det gjeldende elementet).
- Gå til forrige posisjon.
- Når løkken er ferdig (enten ved begynnelsen av arrayet eller ved et element som er mindre), erstatt elementet i gjeldende posisjon med det elementet vi tok ut.
Tidskompleksiteten for innsettingssortering er O(n^2), mens romkompleksiteten er O(1).
Dermed har vi sortert det gitte arrayet. Nå kan vi kjøre koden. Hvis du ikke allerede har installert Python, sjekk ut en installasjonsguide. Du kan også bruke en online Python-kompilator.
def insertion_sort(arr, n):
for i in range(1, n):
current_position = i
current_element = arr[i]
while current_position > 0 and current_element < arr[current_position - 1]:
arr[current_position] = arr[current_position - 1]
current_position -= 1
arr[current_position] = current_element
if __name__ == '__main__':
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
insertion_sort(arr, 9)
print(str(arr))
Utvalgssortering
Utvalgssortering har likheter med innsettingssortering, men med en liten forskjell. Også her deles arrayet inn i en sortert og en usortert del. I hver iterasjon finner vi minimumselementet i den usorterte delen og plasserer det sist i den sorterte delen.
La oss visualisere utvalgssortering for å forstå den bedre.
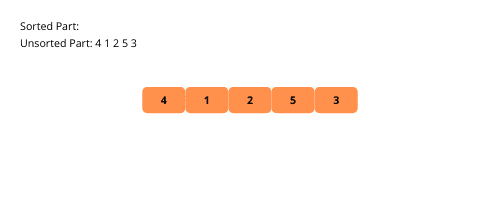
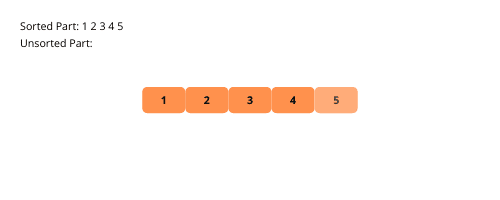
Her er fremgangsmåten for implementering av utvalgssortering:
- Initialiser arrayet med testdata (heltall).
- Gå gjennom arrayet.
- Lagre indeksen til minimumselementet.
- Start en løkke som går fra det gjeldende elementet til slutten av arrayet.
- Sjekk om det gjeldende elementet er mindre enn det som er lagret som minimumselementet.
- Hvis det gjeldende elementet er mindre, oppdaterer du indeksen til minimumselementet.
- Når vi har funnet indeksen til minimumselementet, bytter vi det gjeldende elementet med dette minimumselementet.
Tidskompleksiteten for utvalgssortering er O(n^2), mens romkompleksiteten er O(1).
Prøv å implementere algoritmen selv, siden den har likhetstrekk med innsettingssortering. Koden finner du nedenfor:
def selection_sort(arr, n):
for i in range(n):
min_element_index = i
for j in range(i + 1, n):
if arr[j] < arr[min_element_index]:
min_element_index = j
arr[i], arr[min_element_index] = arr[min_element_index], arr[i]
if __name__ == '__main__':
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
selection_sort(arr, 9)
print(str(arr))
Boblesortering
Boblesortering er en enkel algoritme som gjentatte ganger bytter om på tilstøtende elementer til arrayet er sortert.
Den går gjennom arrayet og flytter det gjeldende elementet til neste posisjon så lenge det er mindre enn det neste elementet.
La oss se noen illustrasjoner for å få en visuell forståelse av boblesortering.
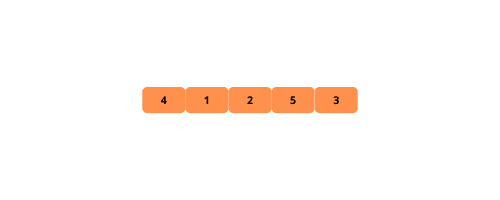
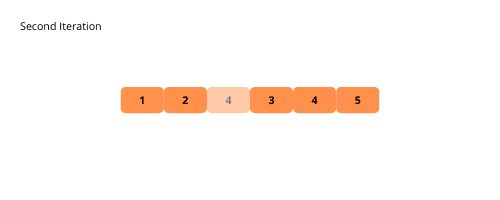
Fremgangsmåten for å implementere boblesortering er som følger:
Tidskompleksiteten for boblesortering er O(n^2), og romkompleksiteten er O(1).
Du kan nå enkelt implementere boblesortering. Her er koden:
def bubble_sort(arr, n):
for i in range(n):
for j in range(n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
if __name__ == '__main__':
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
bubble_sort(arr, 9)
print(str(arr))
Flettesortering
Flettesortering er en rekursiv algoritme for å sortere et array. Den er mer effektiv enn de tidligere nevnte algoritmene når det gjelder tidskompleksitet. Den bruker «del og hersk»-prinsippet.
Algoritmen deler arrayet i to halvdeler, sorterer dem separat og slår dem deretter sammen til et enkelt sortert array.
Siden det er en rekursiv algoritme, deler den arrayet helt til det enkleste tilfellet (et array med ett element) som er trivielt å sortere.
La oss se en illustrasjon.
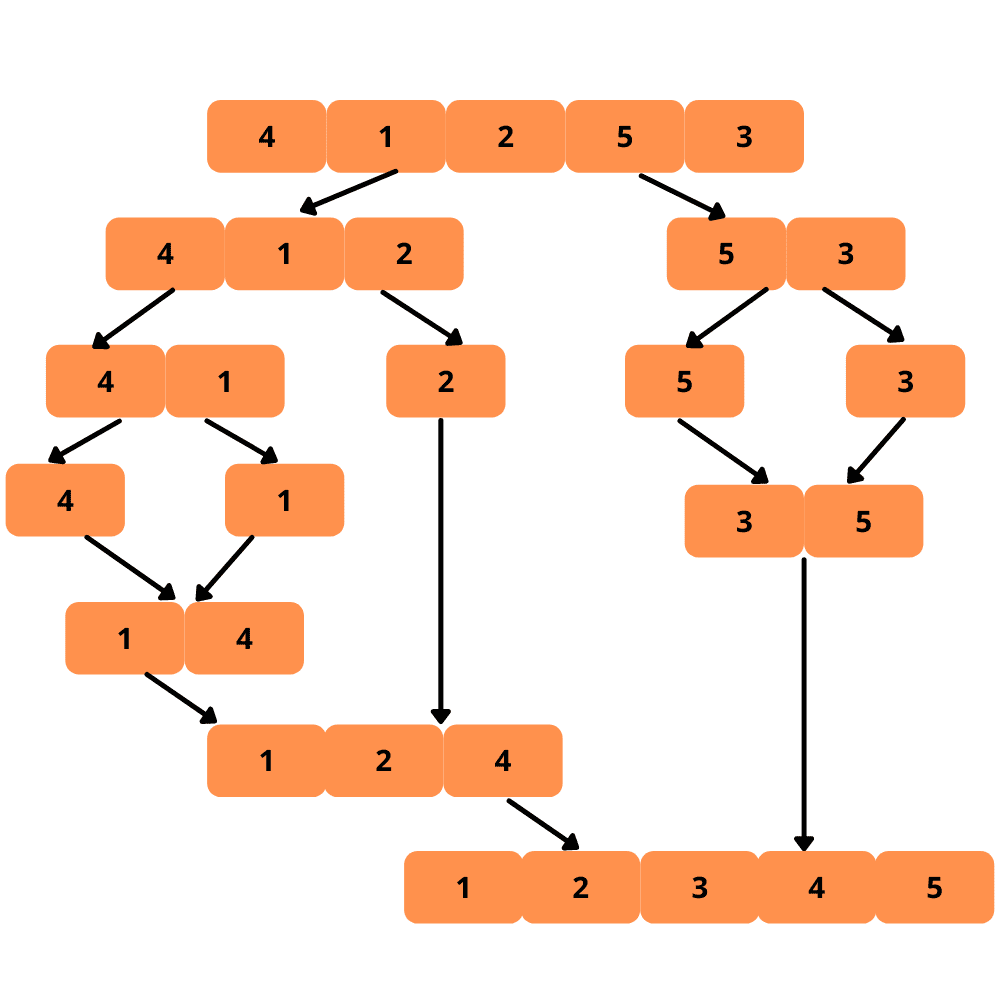
Fremgangsmåten for å implementere flettesortering er som følger:
- Initialiser arrayet med testdata (heltall).
- Lag en funksjon kalt «flette» som slår sammen to sorterte under-array til ett enkelt sortert array. Den tar som input arrayet, venstre, midt og høyre indekser.
- Beregn lengdene til venstre og høyre under-array.
- Kopier elementene fra arrayet til de respektive venstre og høyre arrayene.
- Gå gjennom de to under-arrayene.
- Sammenlign elementene fra de to under-arrayene.
- Erstatt elementet i hoved-arrayet med det minste elementet fra de to under-arrayene.
- Sjekk om det er elementer igjen i de to under-arrayene.
- Legg til de resterende elementene i hoved-arrayet.
- Lag en funksjon kalt «merge_sort» som tar som input arrayet og venstre og høyre indekser.
- Hvis venstre indeks er større eller lik høyre indeks, returner.
- Finn midtpunktet av arrayet for å dele arrayet i to halvdeler.
- Kall «merge_sort» rekursivt ved hjelp av venstre, høyre og midt-indeksene.
- Etter de rekursive kallene, slå sammen arrayet ved hjelp av «flette»-funksjonen.
Tidskompleksiteten til flettesortering er O(n log n), mens romkompleksiteten er O(n).
Det var det for implementasjonen av flettesorteringsalgoritmen. Sjekk koden nedenfor:
def merge(arr, left_index, mid_index, right_index):
left_array = arr[left_index:mid_index+1]
right_array = arr[mid_index+1:right_index+1]
left_array_length = mid_index - left_index + 1
right_array_length = right_index - mid_index
i = j = 0
k = left_index
while i < left_array_length and j < right_array_length:
if left_array[i] < right_array[j]:
arr[k] = left_array[i]
i += 1
else:
arr[k] = right_array[j]
j += 1
k += 1
while i < left_array_length:
arr[k] = left_array[i]
i += 1
k += 1
while j < right_array_length:
j += 1
k += 1
def merge_sort(arr, left_index, right_index):
if left_index >= right_index:
return
mid_index = (left_index + right_index) // 2
merge_sort(arr, left_index, mid_index)
merge_sort(arr, mid_index + 1, right_index)
merge(arr, left_index, mid_index, right_index)
if __name__ == '__main__':
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
merge_sort(arr, 0, 8)
print(str(arr))
Konklusjon
Det finnes mange flere sorteringsalgoritmer, men de vi har gått gjennom her er blant de mest brukte. Vi håper du har funnet denne presentasjonen av sorteringsalgoritmer nyttig.
Neste steg kan være å utforske ulike søkealgoritmer.
Lykke til med kodingen! 🙂 👨💻