I denne veiledningen skal vi utforske hvordan man multipliserer to matriser ved hjelp av Python.
Vi begynner med å se på kravene for en gyldig matrisemultiplikasjon, og vi utvikler en skreddersydd Python-funksjon for å utføre denne operasjonen. Deretter skal vi se hvordan vi kan oppnå det samme resultatet med bruk av nestede listeforståelser.
Til sist, vi går over til å benytte NumPy og dens innebygde funksjoner for å effektivisere matrisemultiplikasjonen.
Slik sjekker du gyldigheten av matrisemultiplikasjon
Før vi dykker ned i Python-koden, er det viktig å friske opp de grunnleggende prinsippene for matrisemultiplikasjon.
Multiplikasjon av to matriser, A og B, er kun mulig dersom antallet kolonner i matrise A tilsvarer antallet rader i matrise B.
Du har kanskje støtt på denne regelen tidligere. Men har du noen gang reflektert over *hvorfor* dette er nødvendig?
Grunnen ligger i selve mekanismen for matrisemultiplikasjon. Ta en titt på illustrasjonen nedenfor.
I dette generiske eksemplet har matrise A «m» antall rader og «n» antall kolonner. Matrise B har «n» antall rader og «p» antall kolonner.
Hva er dimensjonene til den resulterende matrisen?
Elementet ved posisjon (i, j) i den resulterende matrisen C er gitt ved prikkproduktet av rad «i» i matrise A og kolonne «j» i matrise B.
For å finne et bestemt element i den resulterende matrisen C, må vi altså beregne prikkproduktet av den tilsvarende raden og kolonnen fra henholdsvis matrisene A og B.
Ved å gjenta denne prosessen, får vi produktmatrisen C med dimensjonene mxp – bestående av «m» rader og «p» kolonner, som illustrert nedenfor.
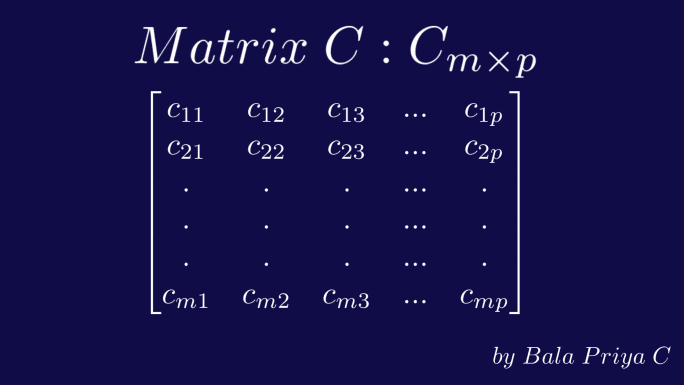
Prikkproduktet eller det indre produktet mellom to vektorer a og b beregnes med følgende formel:

La oss oppsummere det vi har sett på:
- Det er klart at prikkproduktet bare er definert for vektorer med lik lengde.
- For at prikkproduktet mellom en rad og en kolonne skal være gyldig når vi multipliserer to matriser, må begge ha samme antall elementer.
- I eksemplet ovenfor har hver rad i matrise A «n» elementer. Likeledes har hver kolonne i matrise B også «n» elementer.
Når vi ser nærmere etter, innser vi at «n» er antall kolonner i matrise A og samtidig antall rader i matrise B. Dette er nøyaktig grunnen til at antall kolonner i A må samsvare med antall rader i B.
Jeg håper du nå forstår betingelsene for en gyldig matrisemultiplikasjon og hvordan man beregner hvert element i den resulterende matrisen.
La oss nå gå videre til å skrive Python-kode for å utføre matrisemultiplikasjon.
Lag en tilpasset Python-funksjon for matrisemultiplikasjon
La oss starte med å lage en funksjon som utfører matrisemultiplikasjon.
Denne funksjonen skal:
- Ta to matriser, A og B, som input.
- Verifisere om multiplikasjon mellom A og B er gyldig.
- Dersom det er gyldig, multipliser matrisene A og B, og returnere den resulterende matrisen C.
- Ellers returnere en feilmelding som indikerer at matrisene A og B ikke kan multipliseres.
Trinn 1: Generer to matriser med heltall ved hjelp av NumPys random.randint() funksjon. Det er også mulig å deklarere matriser som nestede Python-lister.
import numpy as np
np.random.seed(27)
A = np.random.randint(1,10,size = (3,3))
B = np.random.randint(1,10,size = (3,2))
print(f"Matrix A:n {A}n")
print(f"Matrix B:n {B}n")
# Output
Matrix A:
[[4 9 9]
[9 1 6]
[9 2 3]]
Matrix B:
[[2 2]
[5 7]
[4 4]]
Trinn 2: Definer funksjonen `multipliser_matrise(A,B)`. Funksjonen mottar to matriser, A og B, og returnerer produktmatrisen C dersom multiplikasjonen er mulig.
def multiply_matrix(A,B):
global C
if A.shape[1] == B.shape[0]:
C = np.zeros((A.shape[0],B.shape[1]),dtype = int)
for row in range(rows):
for col in range(cols):
for elt in range(len(B)):
C[row, col] += A[row, elt] * B[elt, col]
return C
else:
return "Beklager, A og B kan ikke multipliseres."
Analyse av funksjonsdefinisjonen
La oss se nærmere på hva som skjer i funksjonen.
Erklær C som en global variabel: Som standard har variabler i en Python-funksjon et lokalt omfang, og de er utilgjengelige utenfor funksjonen. For å gjøre produktmatrisen C tilgjengelig utenfor funksjonen, må vi definere den som en global variabel. Dette gjøres ved å legge til nøkkelordet `global` foran variabelnavnet.
Sjekk om matrisemultiplikasjon er gyldig: Vi bruker `shape`-attributtet for å sjekke om A og B kan multipliseres. For en hver array `arr`, angir `arr.shape[0]` og `arr.shape[1]` henholdsvis antall rader og kolonner. Så `A.shape[1] == B.shape[0]` sjekker om matrisemultiplikasjonen er gyldig. Produktmatrisen vil kun bli beregnet dersom denne betingelsen er sann. Ellers vil funksjonen returnere en feilmelding.
Bruk nestede løkker for å beregne verdier: For å beregne elementene i den resulterende matrisen, må vi gå gjennom radene i matrise A. Den ytre for-løkken tar seg av dette. Den indre for-løkken hjelper oss å iterere gjennom kolonnene i matrise B. Og den innerste for-løkken hjelper oss å få tilgang til hvert element i den valgte kolonnen.
▶️ Nå som vi har sett hvordan Python-funksjonen for å multiplisere matriser fungerer, la oss teste funksjonen med matrisene A og B vi genererte tidligere.
multiply_matrix(A,B)
# Output
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
Siden matrisemultiplikasjon mellom A og B er gyldig, returnerer funksjonen `multiplikasjonsmatrise()` produktmatrisen C.
Bruk nestet listeforståelse for matrisemultiplikasjon
I forrige avsnitt lagde vi en Python-funksjon for matrisemultiplikasjon. Nå skal vi se hvordan vi kan gjøre det samme med nestede listeforståelser.
Her er den nestede listeforståelsen for matrisemultiplikasjon.
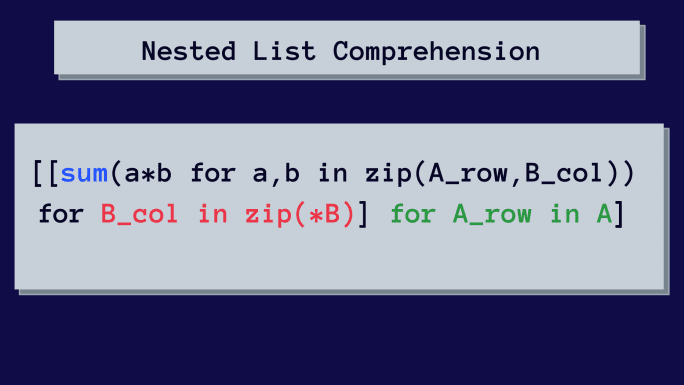
Dette kan se komplisert ut ved første øyekast, men vi vil analysere listeforståelsen steg for steg.
La oss fokusere på en listeforståelse om gangen og identifisere hva den gjør.
Vi bruker følgende generelle mal for listeforståelse:
[<gjør-dette> for <element> in <itererbar>] hvor, <gjør-dette>: det du vil utføre - uttrykk eller operasjon <element>: hvert element du vil utføre operasjonen på <itererbar>: den itererbare (liste, tuppel, etc.) du løkker gjennom
▶️ Sjekk vår guide Listeforståelse i Python – med eksempler for en mer grundig forklaring.
Før vi fortsetter, husk at vi ønsker å bygge den resulterende matrisen C en rad om gangen.
Forklaring av nestet listeforståelse
Trinn 1: Beregn en enkelt verdi i matrisen C
Gitt rad «i» av matrise A og kolonne «j» av matrise B, vil uttrykket nedenfor gi elementet ved indeks (i, j) i matrise C.
sum(a*b for a,b in zip(A_row, B_col) # zip(A_row, B_col) returnerer en iterator av tupler # Hvis A_row = [a1, a2, a3] & B_col = [b1, b2, b3] # zip(A_row, B_col) returnerer (a1, b1), (a2, b2), og så videre
Hvis i = j = 1, vil uttrykket returnere element c_11 i matrise C. På denne måten kan vi beregne et element i en rad.
Trinn 2: Bygg en enkelt rad i matrisen C
Nå er målet å bygge en hel rad.
For rad 1 i matrise A må vi iterere gjennom alle kolonnene i matrise B for å lage en hel rad i matrise C.
La oss gå tilbake til malen for listeforståelse.
- Erstattes <gjør-dette> med uttrykket fra trinn 1, siden det er det vi ønsker å gjøre.
- Deretter erstatter vi <element> med `B_col`—hver kolonne i matrise B.
- Til slutt erstatter vi <itererbar> med `zip(*B)` – listen som inneholder alle kolonnene i matrise B.
Her er den første listeforståelsen.
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] # zip(*B): * er utpakkingsoperatoren # zip(*B) returnerer en liste med kolonnene i matrise B
Trinn 3: Bygg alle radene og konstruer matrise C
Nå må vi fylle ut hele produktmatrisen C ved å beregne de resterende radene.
For dette må vi iterere gjennom alle radene i matrise A.
Gå tilbake til listeforståelsen igjen, og gjør følgende:
- Erstattes <gjør-dette> med listeforståelsen fra trinn 2. Husk at vi beregnet en hel rad i forrige trinn.
- Erstattes <element> med `A_row` – hver rad i matrise A.
- Og <itererbar> er matrise A, der vi iteres gjennom radene.
Her er vår endelige nestede listeforståelse.🎊
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A]
Nå er det på tide å verifisere resultatet! ✔
# konverter til <a href="https://tipsbilk.net.com/numpy-reshape-arrays-in-python/">NumPy array</a> ved hjelp av np.array()
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A])
# Output:
[[ 89 107]
[ 47 49]
[ 40 44]]
Om du ser nøye etter, er dette ekvivalent med de nestede for-løkkene vi hadde tidligere, bare mer konsist.
Vi kan også gjøre dette enda mer effektivt ved å benytte noen innebygde funksjoner. La oss lære om dem i neste avsnitt.
Bruk NumPy `matmul()` for matrisemultiplikasjon i Python
`np.matmul()` tar inn to matriser som input og returnerer produktet dersom multiplikasjonen er gyldig.
C = np.matmul(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]
Legg merke til hvor mye enklere denne metoden er i forhold til de to foregående. I tillegg til `np.matmul()`, kan vi bruke den tilsvarende @-operatoren, som vi skal demonstrere straks.
Hvordan bruke @-operatoren i Python for matrisemultiplikasjon
I Python er `@` en binær operator som brukes til matrisemultiplikasjon.
Den opererer på to matriser, og generelt N-dimensjonale NumPy-arrays, og returnerer produktmatrisen.
Merk: Du må ha Python 3.5 eller nyere for å bruke @-operatoren.
Slik brukes den.
C = A @ B
print(C)
# Output
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])
Legg merke til at produktmatrisen C er den samme som den vi har sett tidligere.
Kan du bruke `np.dot()` for matrisemultiplikasjon?
Hvis du har kommet over kode som bruker `np.dot()` til å multiplisere to matriser, så fungerer det slik.
C = np.dot(A,B) print(C) # Output: [[ 89 107] [ 47 49] [ 40 44]]
Vi ser at `np.dot(A, B)` også returnerer den forventede produktmatrisen.
Men ifølge NumPy-dokumentasjonen, bør du kun bruke `np.dot()` for å beregne prikkproduktet av to endimensjonale vektorer, og ikke for matrisemultiplikasjon.
Husk fra tidligere at elementet ved posisjon (i, j) i produktmatrisen C er prikkproduktet av rad «i» i matrise A og kolonne «j» i matrise B.
Siden NumPy implisitt utvider denne prikkproduktoperasjonen til alle rader og alle kolonner, får vi den resulterende matrisen. For å holde koden lettleselig og unngå tvetydighet, anbefales det imidlertid å bruke `np.matmul()` eller @-operatoren isteden.
Konklusjon
🎯 I denne opplæringen har vi lært følgende:
- Kravet for en gyldig matrisemultiplikasjon: antall kolonner i matrise A = antall rader i matrise B.
- Hvordan lage en tilpasset Python-funksjon som verifiserer om matrisemultiplikasjonen er gyldig og returnerer produktmatrisen. Hoveddelen av funksjonen bruker nestede for-løkker.
- Hvordan bruke nestede listeforståelser for å multiplisere matriser. De er mer konsise enn for-løkker, men kan være mindre lesbare.
- Hvordan bruke NumPy-funksjonen `np.matmul()` for matrisemultiplikasjon, og hvordan dette er den mest effektive metoden med tanke på hastighet.
- Vi har også sett på hvordan man kan bruke @-operatoren for å multiplisere to matriser i Python.
Dette avslutter vår diskusjon om matrisemultiplikasjon i Python. Som et neste steg kan du lære hvordan du sjekker om et tall er et primtall i Python. Eller utforske interessante problemer med Python-strenger.
Lykke til med læringen!🎉