«`html
Hypotesetesting er en fremgangsmåte som benyttes av mange analytikere, både i privat og offentlig sektor, for å formulere velbegrunnede påstander eller antakelser om data fra befolkningen.
Dersom du har jobbet med eller studert befolkningsdata, har du sannsynligvis støtt på dette essensielle verktøyet for hypotesetesting.
Det finnes en rekke metoder for å gjøre antakelser, men ikke alle sikrer høy grad av nøyaktighet.
Hvis du er usikker på datagrunnlaget, men likevel ønsker å anvende det, kan dette medføre risiko for organisasjonen din.
Hypotesetesting er en effektiv strategi for å oppnå større presisjon. Den har spilt en sentral rolle i analyse av befolkningsdata.
I denne artikkelen vil jeg redegjøre for hva hypotesetesting innebærer, hvordan det fungerer, fordelene ved å bruke det, samt praktiske eksempler.
La oss komme i gang!
Hva er hypotesetesting?
Hypotesetesting er en statistisk metode som analytikere bruker for å undersøke om tilgjengelige data fra en populasjon i tilstrekkelig grad underbygger en gitt hypotese, og for å trekke slutninger basert på dette.
Gjennom denne metoden kan analytikere enkelt evaluere en hypotese og vurdere hvor nøyaktig antagelsen er, ut fra de tilgjengelige dataene.
Enkelt forklart er det en testprosess basert på statistiske konklusjoner, som muliggjør en vurdering av populasjonsdata basert på innsamlede prøvedata.
Generelt sett er det nesten umulig for analytikere å kartlegge egenskaper eller en bestemt parameter for hele befolkningen. Men ved hjelp av hypotesetesting kan man likevel gjøre en informert prediksjon og ta beslutninger basert på prøvedataenes nøyaktighet.
Typer hypotesetesting
De ulike formene for hypotesetesting inkluderer:
- Nullhypotese: Statistisk sett indikerer dette at prøvedataene er tilfeldige, og at det ikke foreligger noen korrelasjon mellom de to variablene i de gitte prøvedataene.
- Alternativ hypotese: Dette presenterer hovedantagelsen og står i motsetning til nullhypotesen. Det er den viktigste faktoren i testprosessen, da den viser en korrelasjon mellom to variabler i prøvedataene.
- Ikke-retningsbestemt hypotese: Denne formen for hypotesetesting fungerer som en tosidig hypotese. Den viser at det ikke er noen bestemt retning i forholdet mellom to variabler i prøvedataene, og at den faktiske verdien ikke er den samme som den forventede.
- Retningsbestemt hypotese: Dette antyder en relasjon mellom to variabler. Her kan en variabel i et datasett påvirke andre variabler.
- Statistisk hypotese: Dette hjelper analytikere med å evaluere om dataene og verdien bekrefter en gitt hypotese. Dette er svært nyttig for å formulere påstander og antagelser om resultatet av en prøvepopulasjonsparameter.
La oss nå se på metodene for hypotesetesting.
Metoder for hypotesetesting
For å kunne avgjøre om en spesifikk hypotese er sann eller ikke, vil du som analytiker trenge et solid bevisgrunnlag for å kunne konkludere. I denne prosessen formuleres en nullhypotese og en alternativ hypotese før selve evalueringen starter.
Hypotesetesting omfatter en rekke metoder for å vurdere om prøvedataene er hensiktsmessige. Som analytiker må du analysere dataene og prøvestørrelsen for å velge den hypotesetestmetoden som er mest passende.
Normalitetstesting
Dette er en standardmetode for hypotesetesting som brukes for å analysere den normale fordelingen i prøvedata. Under denne prosessen sjekkes det om de grupperte datapunktene rundt gjennomsnittet ligger under eller over gjennomsnittet.
I denne statistiske testen er sannsynligheten for at punktene går over eller under gjennomsnittet like stor. Det dannes en klokkeformet kurve, og den er likt fordelt på begge sider av gjennomsnittet.
Z-Test testing
Dette er en annen form for hypotesetesting som benyttes når populasjonsdataene er normalfordelt. Den tester om gjennomsnittet av to separate populasjonsparametre er forskjellig når variansen til dataene er kjent.
Ved analyse av populasjonsdata, vil denne metoden som oftest benyttes når dataprøvestørrelsen er over tretti. I tillegg er den sentrale grensesetningen en annen årsak til at Z-Test er egnet, da teoremet sier at når prøvestørrelsene øker, blir prøvene normalfordelt.
T-test testing
T-Test hypotesetesting brukes når prøvestørrelsen er begrenset og normalfordelt. Den brukes i hovedsak når prøvestørrelsen er under 30, og standardavviket til parameteren er ukjent.
Når du gjennomfører en T-test, gjør du dette for å beregne konfidensintervallene til spesifikke populasjonsdata.
Chi-Square Test
Chi-kvadrat-testen er en mye brukt prosess for hypotesetesting, som ofte anvendes for å vurdere egnetheten og integriteten til en datadistribusjon.
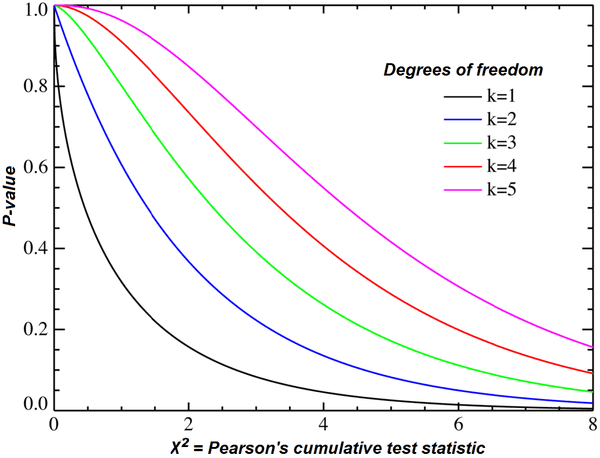 Kilde: wikipedia.org
Kilde: wikipedia.org
Hovedårsaken til at du bør benytte denne hypotesetypen, er når du skal teste populasjonsvariansen opp mot en populasjonsvarians med en antatt eller kjent verdi. Det utføres forskjellige Chi-Square-tester, men den mest brukte typen er Chi-Square-testen for varians og uavhengighet.
ANOVA-testing

ANOVA, forkortet for Analysis of Variance, er en statistisk testmetode som hjelper til med å sammenligne datasettene til to prøver. Metoden gir imidlertid mulighet til å sammenligne mer enn to metoder samtidig.
Den forklarer også en avhengig variabel og en uavhengig variabel ut fra prøvedata. Bruken av ANOVA er ganske lik bruken av Z-Test og T-Test, men de to sistnevnte er begrenset til kun to sammenligningsgrunnlag.
Hvordan fungerer hypotesetesting?
Enhver analytiker som benytter hypotesetesting, bruker tilfeldige prøvedata for analyse og måling. Under testingen brukes tilfeldige prøvedata for å teste nullhypotesen og den alternative hypotesen.
Som nevnt tidligere, er nullhypotesen og den alternative hypotesen gjensidig utelukkende, og kun én av dem kan være sann.
Likevel hender det at nullhypotesen forkastes; den alternative hypotesen er ikke alltid sann.
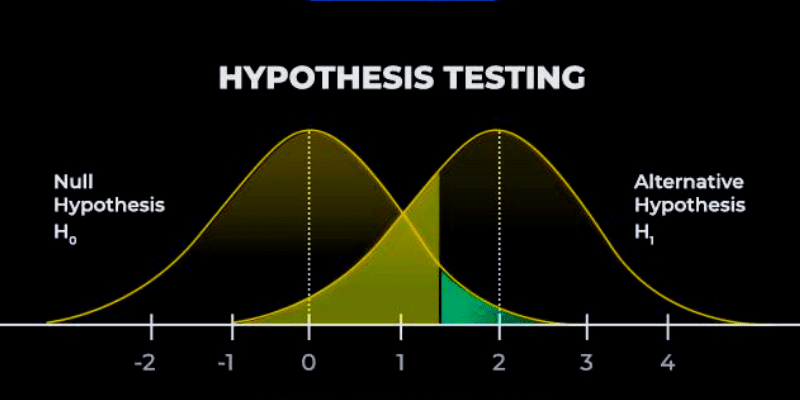 Kilde: Analytics Steps
Kilde: Analytics Steps
p-verdi: I testprosessen er p-verdien, eller sannsynlighetsverdien, viktig. Den indikerer om resultatet er signifikant eller ikke. p-verdien viser også sannsynligheten for feil ved å avvise eller ikke avvise en nullhypotese under testingen. Den resulterende p-verdien er enten 0 eller 1, som deretter sammenlignes med signifikansnivået eller alfanivået.
Signifikansnivået angir den akseptable risikoen ved forkasting av en nullhypotese under testingen. Det er viktig å huske på at resultatet av hypotesetesten kan føre til to typer feil:
- Type 1-feil oppstår når testresultatet avviser nullhypotesen, selv om den er sann.
- Type 2-feil oppstår når nullhypotesen aksepteres av prøveresultatet, til tross for at den er usann.
Alle verdier som fører til at nullhypotesen avvises, er lagret i det kritiske området. Det er den kritiske verdien som skiller de kritiske regionene fra andre.
Trinn for å utføre hypotesetesting
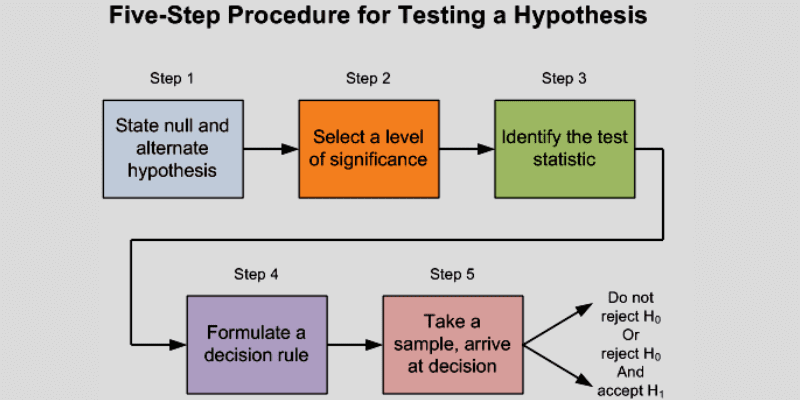 Kilde: Medium
Kilde: Medium
Hypotesetesting innebærer hovedsakelig fire trinn:
- Definer hypoteser: I det første trinnet definerer analytikeren to hypoteser, hvorav kun én kan være sann. Nullhypotesen vil indikere at det ikke er noen forskjell i gjennomsnittlig BMI, mens den alternative hypotesen vil hevde at det er en signifikant forskjell i gjennomsnittlig BMI.
- Plan: I neste trinn må det utarbeides en analyseplan for hvordan prøvedataene skal analyseres. Det er viktig at prøvetakingen gjennomføres og at prøvedataene samles inn på en slik måte at det sikres at de er egnet for å teste hypotesen.
- Analyser prøvedata: Etter at det er bestemt hvordan dataene skal evalueres, er det tid for selve analysen. Prøvedataene må analyseres grundig for å unngå overflødig informasjon. Underveis bør det kontrolleres at prøvene er uavhengige av hverandre, og at begge prøvestørrelsene er tilstrekkelig store.
- Beregn teststatistikk: På dette stadiet beregnes teststatistikken og p-verdien. P-verdien bestemmes ved å anta at nullhypotesen er sann.
- Evaluer resultatet: I det siste trinnet må resultatet av hypotesetesten evalueres. Det må avgjøres om nullhypotesen skal forkastes eller om dens sannsynlighet skal bekreftes, basert på prøvedataene.
Nå skal vi se på fordelene ved hypotesetesting.
Fordeler med hypotesetesting
Fordelene med hypotesetesting er:
- Det bidrar til å analysere styrken i et krav knyttet til en databasert beslutning.
- Som analytiker kan du skape et pålitelig miljø for å beslutte ut fra prøvedata.
- Metoden lar deg fastslå om prøvedataene som inngår i hypotesetesting er statistisk signifikante.
- Hypotesetesting er nyttig for å vurdere påliteligheten og validiteten til testresultater i en systematisk testprosess.
Det bidrar til å ekstrapolere data fra en prøvefase til en større populasjon, avhengig av kravet.
Bruksområder for hypotesetesting
Hypotesetesting benyttes i ulike sektorer for å vurdere nøyaktigheten av prøvedata. Noen eksempler fra virkeligheten på bruk av hypotesetesting er:
#1. Kliniske studier
Hypotesetesting er mye brukt i kliniske studier, da det hjelper medisinsk personell med å avgjøre om et nytt legemiddel, behandling eller prosedyre vil være effektiv eller ikke, basert på prøvedata.
En lege kan for eksempel anta at en behandling kan redusere kaliumnivået hos enkelte pasienter. Legen kan måle kaliumnivået til en gruppe pasienter før behandlingen og kontrollere nivået på nytt.

Legen gjennomfører deretter hypotesetesting med H0: Uetter = Ubefore, som indikerer at kaliumnivået er uendret etter behandlingen. En alternativ hypotese kan være Ha: Uafter < Ubefore, som betyr at kaliumnivået har gått ned etter behandlingen.
Dersom p-verdien er lavere enn signifikansnivået, kan legen konkludere med at behandlingen kan redusere kaliumnivået.
#2. Produksjon
Hypotesetesting brukes i produksjonsanlegg for å hjelpe veiledere med å avgjøre om en ny metode eller teknikk er effektiv eller ikke.
For eksempel kan en produksjonsenhet bruke hypotesetesting for å finne ut om en ny metode bidrar til å redusere antall defekte produkter per parti. Anta at antall defekte produkter er 300 per parti.

Produsenten må bestemme gjennomsnittet for det totale antall defekte produkter produsert før og etter bruk av metoden. De kan utføre hypotesetesting og bruke hypotesene H0: Uafter = Ubefore, der gjennomsnittet av defekte produkter etter bruk av en ny metode er det samme som før.
En annen hypotese viser at HA: Uafter ikke er lik Ubefore, noe som betyr at det totale antall defekte produkter produsert etter bruk av den nye metoden har endret seg.
Etter testen, når p-verdien er lavere enn signifikansnivået, kan produksjonsenheten konkludere med at antall produserte defekte produkter har endret seg.
#3. Jordbruk
Hypotesetesting benyttes ofte for å vurdere om gjødsel eller plantevernmidler påvirker vekst og motstandskraft hos planter. Biologer kan bruke testen for å bevise at en plante kan vokse mer enn 15 tommer etter påføring av den nye gjødselen.

Biologen kan bruke gjødsel i en måned for å samle inn prøvedata. Når biologen utfører en test, er en hypotese H0 U=15 tommer, som indikerer at gjødselen ikke har noen effekt på plantenes gjennomsnittlige vekst.
En annen hypotese viser HA: U> 15 tommer, som betyr at gjødselen bidrar til økt gjennomsnittlig vekst. Etter testing kan biologen bevise at gjødselen gir mer vekst enn tidligere, forutsatt at p-verdien er lavere enn signifikansnivået.
Læringsressurser
#1. Statistikk: En trinnvis introduksjon fra Udemy

Udemy tilbyr et kurs i statistikk der du får en trinnvis introduksjon til statistikk, inkludert hypotesetesting. Kurset inneholder eksempler og leksjoner fra en tidligere dataforsker fra Google, som skal hjelpe deg med å mestre konfidensintervaller, hypotesetester med mer.
#2. Viktig statistikk for dataanalyse fra Udemy
Dette Udemy-kurset om viktig statistikk for dataanalyse hjelper deg med å lære statistikk ved hjelp av virkelige prosjekter, morsomme aktiviteter, hypotesetester, sannsynlighetsfordelinger, regresjonsanalyse med mer.
#3. Statistikk for datavitenskap og forretningsanalyse

Dette Udemy-kurset om statistikk for datavitenskap og forretningsanalyse hjelper deg med å lære hypotesetesting. Det dekker ulike statistikkemner som er relevante for dataforskere og forretningsanalytikere. Det omfatter både inferensiell og beskrivende statistikk, samt regresjonsanalyse.
#4. Hypotesetesting av Jim Frost
Denne boken er tilgjengelig på Amazon og er en intuitiv guide som hjelper analytikere med å ta datadrevne beslutninger.
Den tar for seg hvordan hypotesetester fungerer, hvorfor de er nødvendige, hvordan du effektivt bruker konfidensintervaller, p-verdier, signifikansnivåer og mange andre relevante emner.
#5. Hypotesetesting av Scott Hartshorn
Denne boken er unik med sine visuelle eksempler og er best egnet for nybegynnere som ønsker en rask innføring i hypotesetesting.
Den introduserer deg for betydningen av statistikk, ulike typer og hvordan de fungerer. Det krever ikke dybdekunnskap på forhånd, men forklarer alt på en intuitiv måte.
Avslutningsvis
Hypotesetesting bidrar til å bekrefte en antagelse og deretter utvikle statistiske data basert på vurderingen. Det brukes i mange sektorer, fra produksjon og landbruk til kliniske studier og IT. Denne metoden er ikke bare nøyaktig, men hjelper deg også med å ta datadrevne beslutninger for organisasjonen din.
Du kan gjerne sjekke de nevnte læringsressursene for å utvikle deg som forretningsanalytiker.
«`