Denne veiledningen gir deg kunnskap om hvordan du utvikler et Python-program for å avgjøre om et gitt tall er et primtall eller ikke.
Dersom du noen gang har deltatt i programmeringsprøver, har du muligens kommet over matematiske problemstillinger som krever at du tester for primtall. I de neste minuttene vil du bli veiledet i å finne den mest effektive løsningen for dette problemet.
I denne veiledningen vil du:
- Få en repetisjon av grunnleggende kunnskap om primtall,
- Skrive Python-kode for å identifisere om et tall er et primtall, og
- Optimalisere koden for å oppnå en algoritme med O(√n) tidskompleksitet.
La oss begynne å utforske alt dette og mer.
Hva definerer et primtall?
La oss starte med å repetere det grunnleggende om primtall.
I tallteori defineres et naturlig tall n som prim hvis det har nøyaktig to faktorer: 1 og tallet selv (n). Et tall i anses som en faktor av n hvis i deler n uten rest. ✅
Tabellen nedenfor illustrerer noen tall, deres faktorer, og om de er primtall.
| n | Faktorer | Primtall? |
| 1 | 1 | Nei |
| 2 | 1, 2 | Ja |
| 3 | 1, 3 | Ja |
| 4 | 1, 2, 4 | Nei |
| 7 | 1, 7 | Ja |
| 15 | 1, 3, 5, 15 | Nei |
Fra tabellen kan vi utlede følgende:
- 2 er det laveste primtallet.
- 1 er en faktor for alle tall.
- Et hvert tall n er en faktor av seg selv.
Dermed er 1 og n de opplagte faktorene for et hvilket som helst tall n. Et primtall har ingen andre faktorer enn disse to.
Dette betyr at når vi undersøker tall fra 2 til n – 1, skal vi ikke finne en faktor som deler n uten rest.
O(n) Algoritme for primtallstest i Python
La oss formalisere den ovennevnte tilnærmingen i en Python-funksjon.
Vi kan sjekke alle tall fra 2 til n – 1 ved hjelp av `range()` i Python.
I Python gir `range(start, stop, step)` et range-objekt, som vi kan iterere over for å få en sekvens av tall fra `start` opp til `stop – 1` med angitt `step`.
Siden vi trenger heltallene fra 2 til n – 1, kan vi spesifisere `range(2, n)` og bruke den i en `for`-løkke.
Vi skal gjøre følgende:
- Hvis vi finner et tall som deler n jevnt uten rest, kan vi umiddelbart konkludere med at tallet ikke er et primtall.
- Hvis vi har gått gjennom alle tall fra 2 til n – 1 uten å finne et tall som deler n uten rest, er tallet et primtall.
Python-funksjon for primtallstest
Med utgangspunkt i det ovennevnte, kan vi definere funksjonen `is_prime()` som følger:
def is_prime(n):
for i in range(2,n):
if (n%i) == 0:
return False
return True
La oss analysere denne funksjonsdefinisjonen:
- Funksjonen `is_prime()` tar et positivt heltall n som argument.
- Dersom en faktor finnes i intervallet (2, n-1), returnerer funksjonen `False` – da er ikke tallet et primtall.
- Den returnerer `True` dersom vi går gjennom hele løkken uten å finne en faktor.
La oss teste funksjonen med noen argumenter og verifisere resultatene.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True
Resultatene viser at 2 og 11 er primtall (funksjonen returnerer `True`), mens 8 og 9 ikke er primtall (funksjonen returnerer `False`).
Hvordan optimalisere `is_prime()`?
Vi kan gjøre en liten optimalisering. La oss se på faktorene i tabellen nedenfor.
| Tall | Faktorer |
| 6 | 1, 2, 3, 6 |
| 10 | 1, 2, 5, 10 |
| 18 | 1, 2, 3, 6, 9, 18 |
Vi ser at den eneste faktoren til n som er større enn n/2, er n selv.
Dette betyr at vi ikke trenger å sjekke alle tall opp til n – 1. Vi kan begrense løkken til n/2.
Hvis vi ikke finner en faktor før n/2, vil vi heller ikke finne en etter n/2.
La oss endre `is_prime()` til å lete etter faktorer i intervallet (2, n/2):
def is_prime(n):
for i in range(2,int(n/2)):
if (n%i) == 0:
return False
return True
La oss verifisere output med noen funksjonskall:
is_prime(9) # False is_prime(11) # True
Selv om det kan se ut som om vi har optimalisert, er denne algoritmen ikke mer effektiv enn den forrige med hensyn til tidskompleksitet. Begge har en O(n) tidskompleksitet – proporsjonal med verdien av n, eller lineær i n.
Kan vi gjøre det bedre? Ja, det kan vi!
▶️ Fortsett til neste avsnitt for å lære hvordan vi kan forbedre tidskompleksiteten for primtallstesting.
O(√n) Algoritme for primtallstest i Python
Det viser seg at faktorene til et tall opptrer i par.
Hvis a er en faktor av tallet n, finnes det også en faktor b slik at a * b = n, eller enkelt sagt ab = n.
La oss bekrefte dette med et eksempel.
Tabellen under viser faktorene til tallet 18 som opptrer i par. Du kan bekrefte det samme for andre tall hvis du ønsker.
Vær også oppmerksom på at √18 er ca. 4,24.
I faktorparene (a, b), kan vi se at hvis a er mindre enn 4,24, er b større enn 4,24 – som i dette eksemplet, (2, 18) og (3, 6).
Faktorer av 18 i par:
Hvis tallet n er et perfekt kvadrat, vil a = b = √n være en av faktorene.
▶️ Se på faktorene til 36 i tabellen under. Siden 36 er et perfekt kvadrat, er a = b = 6 en av faktorene. For alle andre faktorpar (a, b), gjelder a < 6 og b > 6.
Faktorer av 36 i par:
Oppsummert gjelder følgende:
- Ethvert tall n kan skrives som n = a * b
- Hvis n er et perfekt kvadrat, så er a = b = √n.
- Hvis a < b, så er a < √n og b > √n.
- Hvis a > b, så er a > √n og b < √n.
I stedet for å sjekke alle heltall opp til n/2, kan vi nøye oss med å sjekke opp til √n. Dette er mye mer effektivt enn vår tidligere tilnærming.
Hvordan endre `is_prime()` til en O(√n) algoritme
La oss optimalisere funksjonen for å sjekke primtall i Python.
import math
def is_prime(n):
for i in range(2,int(math.sqrt(n))+1):
if (n%i) == 0:
return False
return True
La oss analysere denne funksjonsdefinisjonen:
- For å beregne kvadratroten av et tall, importerer vi `math`-modulen i Python og bruker `math.sqrt()`-funksjonen.
- Siden n ikke nødvendigvis er et perfekt kvadrat, må vi konvertere resultatet til et heltall. Bruk `int(var)` for å konvertere `var` til et heltall.
- For å være sikker på at vi sjekker helt opp til √n, legger vi til 1, da `range()`-funksjonen ekskluderer endepunktet som standard.
Koden under bekrefter at funksjonen `is_prime()` fungerer korrekt.
is_prime(8) # False is_prime(15) # False is_prime(23) # True
I neste avsnitt skal vi lage noen enkle grafer for å forstå O(n) og O(√n) visuelt.
Visuell sammenligning av O(n) og O(√n)
▶️ Kjør følgende kodebit i et Jupyter Notebook-miljø.
import numpy as np
import seaborn as sns
import pandas as pd
n = 20
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
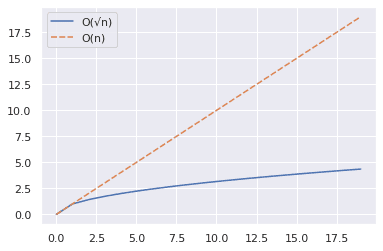
Koden ovenfor viser hvordan vi kan plotte grafene for n og √n for en rekke verdier.
- Vi bruker NumPy-funksjonen `arange()` for å lage en rekke tall.
- Deretter samler vi verdiene for n og √n opp til, men ikke inkludert 20, i en pandas DataFrame.
- Til slutt plotter vi grafen ved hjelp av Seaborns `lineplot()`-funksjon.
Fra grafen under ser vi at √n er betydelig mindre enn n.

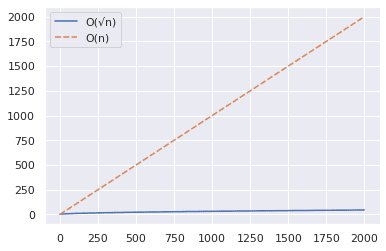
La oss øke intervallet til 2000 og gjenta de samme trinnene.
import numpy as np
import seaborn as sns
import pandas as pd
n = 2000
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

Fra grafen ovenfor kan vi konkludere med at O(√n)-algoritmen er betydelig raskere når vi skal sjekke om et stort tall er et primtall.
Et raskt eksempel: 2377 er et primtall – sjekk selv! 😀
Mens O(n)-tilnærmingen vil kreve ca. 2000 steg, vil O(√n)-algoritmen kunne gi svaret etter bare 49 steg. ✅
Konklusjon
⏳ Det er på tide med en rask oppsummering.
- For å sjekke om et tall er et primtall, er den naive tilnærmingen å sjekke alle tall i intervallet (2, n-1). Hvis vi ikke finner noen faktorer som deler n, er n et primtall.
- Siden den eneste faktoren av n som er større enn n/2 er n selv, kan vi nøye oss med å sjekke opp til n/2.
- Begge de ovennevnte tilnærmingene har en tidskompleksitet på O(n).
- Siden faktorene til et tall opptrer i par, kan vi nøye oss med å sjekke opp til √n. Denne algoritmen er mye raskere enn O(n). Fordelen blir større jo større tall vi tester.
Jeg håper du har fått forståelse for hvordan man tester om et tall er et primtall i Python. Som neste steg, kan du sjekke ut vår veiledning om Python-programmer for strengoperasjoner – hvor du lærer å sjekke om strenger er palindromer, anagrammer og mer.
Vi sees i en annen veiledning. Inntil da, god koding! 👩🏽💻