Kryptering basert på gitterstruktur: En ny tilnærming
Kryptering som baserer seg på gitterstrukturer, fremstår som en avansert metode for å beskytte data ved hjelp av en rekke matematiske prinsipper. Denne teknikken er blitt en viktig del av moderne datasikkerhet.
Kryptografi er en mangfoldig disiplin, og benytter ulike kodingsmetoder for å sikre informasjonen din. Generelt sett innebærer det bruk av komplekse koder for å kryptere data.
Historisk sett var kryptografiske systemer, som krypteringsordninger, ofte utformet uten en solid teoretisk base. Sikkerheten var da i stor grad avhengig av heuristikk og intuisjon.
En av utfordringene er at koder ofte er mer sårbare for å bli brutt. Derfor blir datasikkerhet en vesentlig bekymring for de som velger kodebasert sikkerhetsdesign.
Et annet viktig problem er at mange eksisterende kryptografiske standarder ikke lenger er like pålitelige. Utviklingen av kvantedatamaskiner truer med å svekke disse standardene ytterligere, noe som krever en mer robust tilnærming.
Derfor er det viktig for alle å beskytte personlig informasjon. Dette har ført til behovet for en ny metode som er mer motstandsdyktig mot angrep. Det er behov for forbedrede standarder som kan sikre data også i møte med kvantedatamaskiner.
Etter grundige vurderinger har en ny metode, kalt gitterbasert kryptografi, sett dagens lys.
Denne artikkelen vil utforske gitterbasert kryptografi, betydningen av den, hvordan den fungerer, og andre relevante detaljer.
La oss begynne!
Hva innebærer kryptografi?
Kryptografi er en vitenskap som handler om å sikre kommunikasjon og data gjennom bruk av et bredt spekter av koder. Målet er at informasjonen kun skal være tilgjengelig og lesbar for de som er autorisert. Dermed forhindres uautorisert tilgang til dataene.
Begrepet «kryptografi» er sammensatt av de to greske ordene «krypto» og «graphia».
«Krypto» betyr «skjult», og «graphia» betyr «skriving».
Metodene som brukes for å beskytte informasjonen din er basert på matematiske konsepter og algoritmer som forvandler meldinger til komplekse problemer som er vanskelige å dekode.
Kryptografi deles ofte inn i tre hovedtyper:
- Symmetrisk nøkkelkryptering: Dette innebærer at avsender og mottaker bruker samme nøkkel for å kryptere og dekryptere meldinger. Metoden er raskere og enklere.
- Hash-funksjoner: Denne algoritmen krever ingen nøkkel. En hash-verdi beregnes fra ren tekst, noe som gjør det vanskelig å gjenopprette det opprinnelige innholdet. Metoden brukes ofte til å kryptere passord.
- Asymmetrisk nøkkelkryptering: Her benyttes et par nøkler, en for kryptering og en for dekryptering. Den første er offentlig kjent, mens den andre er privat og kun kjent for mottakeren.
Hva er gitterbasert kryptografi?
Gitterbasert kryptografi er en tilnærming som bygger på bruk av gitterstrukturer i kryptografiske algoritmer. Denne teknikken er viktig i post-kvantekryptografi, designet for å motstå angrep fra kvantedatamaskiner. I motsetning til tradisjonelle ordninger, anses gitterbaserte systemer som mer robuste.
Men hva er egentlig et gitter i denne sammenhengen? Et gitter kan forestilles som et rutenett, på samme måte som i millimeterpapir, som består av punkter plassert med jevne mellomrom. Disse punktene definerer et mønster som kan utvides i det uendelige. Et sett av punkter utgjør en vektor. Utfordringen ligger i å identifisere de punktene som er nærmest et gitt punkt, for eksempel nullpunktet.
Gitterbasert kryptografi benytter komplekse matematiske problemer for å kryptere data, noe som gjør det vanskelig for uvedkommende å bryte sikkerheten og stjele data.
Gitterbasert kryptografi ble først introdusert av Miklos Ajtai i 1996. Sikkerheten var basert på vanskeligheten av gitterproblemer.
I 1998 lanserte Joseph H. Silverman, Jill Pipher og Jeffrey Hoofstein et gitterbasert krypteringssystem med offentlig nøkkel. Imidlertid var ikke dette systemet særlig vanskelig å bryte. I 2005 presenterte Oded Regev det første systemet som var bevist å være motstandsdyktig også i verste fall.
Siden den gang har arbeidet fortsatt med å forbedre effektiviteten. I 2009 introduserte Craig Gentry det første homomorfe krypteringssystemet basert på komplekse gitterproblemer.
Eksempler på implementasjoner er CRYSTALS-Dilithium (digital signatur-algoritme) og CRYSTALS-KYBER (offentlig nøkkelkryptering og nøkkeletablering).
Hvordan fungerer gitterbasert kryptografi?
For å forstå hvordan gitterbasert kryptografi fungerer, la oss se nærmere på noen viktige termer:
- Gitter: Et gitter kan ses på som et rutenett med jevn avstand mellom punkter. Dette mønsteret fortsetter i det uendelige.
- Vektor: En vektor er et punkt, og tallene som representerer det punktet kalles koordinater. For eksempel har vektoren (2,3) koordinatene 2 og 3. Et gitter er en samling av slike vektorer.
- Grunnlag: Gitter kan være store objekter, men datamaskiner har begrenset minne. Derfor bruker man «grunnlaget» for et gitter. Dette er et sett med vektorer som kan brukes for å representere et hvilket som helst punkt i gitteret.
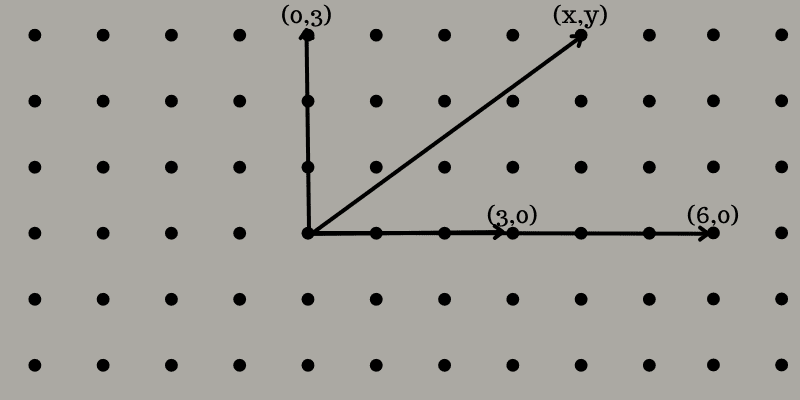
La oss bruke et 2D-gitter som eksempel. Tenk deg et rutenett med punkter på en plan overflate. Velg to punkter som ikke ligger på samme linje gjennom origo.
For eksempel, la oss si (3,0) og (0,3). For å generere et nytt punkt, kan du velge to tall, for eksempel 2 og -1. Multipliser (3,0) med 2, som gir (6,0), og (0,3) med -1, som gir (0,-3). Legg sammen disse resultatene for å få (6,-3).
Med denne metoden kan du generere hele rutenettet med jevnt fordelte punkter, både horisontalt og vertikalt. Koordinatene kan betegnes som (x, y), der x og y er partall, inkludert 0.
Gitter klassifiseres vanligvis i tre kategorier:
- Aperiodisk: Et aperiodisk gitter har et mønster som ikke gjentas nøyaktig, men det er ingen overlappinger eller tomrom.
- Kaotisk: Et kaotisk gitter har overlappinger og tomrom, noe som tilfører tilfeldighet.
- Periodisk: Et periodisk gitter har et mønster som gjentas uten overlappinger eller tomrom.
Hvert gitter fungerer som et mønster der kun de med den riktige vektoren kan dekryptere meldingen. På grunn av de mange mønstrene, er det vanskelig for en angriper å finne det opprinnelige punktet og nøkkelen. Uavhengig av om gitteret har 10 eller 100 punkter, er det bare den som har den riktige nøkkelen som kan dekryptere informasjonen.
Om en angriper prøver å gjette to tilfeldige punkter, vil det være vanskelig å finne ut hvilket punkt i et gitter med 10 punkter som leder til et spesifikt punkt i et gitter med 100 punkter. Dermed, med den korrekte nøkkelen, kan data dekodes med letthet.
Fordeler med gitterbasert kryptografi
Gitterbasert kryptografi tilbyr mange fordeler for både enkeltpersoner og bedrifter.

Lavere energiforbruk
Energiforbruket øker i takt med bruken av et system. Gitterbasert kryptografi, til tross for sin raske beregning, bruker mindre energi sammenlignet med andre metoder. Dette skyldes at den ofte er implementert i maskinvare, noe som gir lavere strømforbruk.
For eksempel, prosessorer som brukes til kryptovaluta-utvinning er mer energieffektive ved bruk av gitterbasert kryptografi enn vanlige prosessorer.
Rask databehandling
Krypteringsprosessen i gitterbasert kryptografi skjer betydelig raskere enn i mange andre kryptografiske algoritmer. Dette resulterer i økt ytelse, og gir raskere respons, noe som er viktig for sanntidsapplikasjoner som online spill og strømming av media.
Enkel implementering og fleksibilitet
Dagens bedrifter søker etter fleksible alternativer. Gitterbasert kryptografi er enkel å implementere da den krever mindre ressurser og er lett tilgjengelig. Den kan i mange tilfeller implementeres med standard utstyr.
Gitterbasert kryptografi brukes også i flere applikasjoner, som digitale signaturer, nøkkelutveksling og passordbasert kryptering. Systemet kan konstrueres på forskjellige måter, noe som gir stor fleksibilitet.
Håndterbare nøkkelstørrelser
Nøklene i gitterbasert kryptografi er små, men ikke like små som i klassiske algoritmer eller kvantesikre isogenibasert systemer. Nøklene kan dermed brukes i standardprotokoller.
Bredt bruksområde

Gitterstrukturer lar brukere løse en rekke sikkerhetsutfordringer, som digitale signaturer og nøkkelutveksling. Det kan også brukes for å skape sikre kanaler for alle ansatte i en organisasjon, for eksempel fullstendig homomorf kryptering og identitetsbasert kryptering.
Matematisk grunnlag
Siden algoritmen er basert på matematiske problemer, er det vanskelig å finne en løsning uten å kjenne nøkkelen. Dette skaper trygghet rundt informasjonssikkerheten.
Forståelighet
Algoritmene som brukes i gitterbasert kryptografi er basert på grunnleggende lineær algebra, noe som krever en mindre kompleks matematisk bakgrunn for å forstå de underliggende prinsippene. Dermed er det mulig å implementere systemet relativt raskt, noe som gir rask sikkerhet og effektivitet.
Ressurser for videre læring
Hvis du ønsker å lære mer om denne teknologien, er det flere bøker og kurs som kan være nyttige. Disse ressursene er tilgjengelige online og kan hjelpe deg med å bli en ekspert innen sikkerhet. La oss se nærmere på noen av disse:

#1. Lattice-Based Cryptosystems: A Design Perspective
Boken er skrevet av Jiang Zhang og Zhenfeng Zhang, og fokuserer på de gitterbaserte kryptosystemene som anses som lovende post-kvante-systemer. Boken gir en innføring i hvordan man bygger et sikkerhetslag basert på gitterproblemer.
Hovedmålet er å gi leseren verktøyene som er nødvendig for å velge riktige gitterstrukturer for kryptosystemer. Dette inkluderer design av attributtbasert kryptering, digitale signaturer, nøkkelutveksling, identitetsbasert kryptering og offentlig nøkkelkryptering.
#2. Lattice-Based Public Key Cryptography in Hardware
Denne boken, forfattet av Sujoy Sinha Roy og Ingrid Verbauwhede, beskriver implementeringen av offentlig nøkkelkryptering. De tar for seg sikkerhetsutfordringer knyttet til store datamengder, generert av nettverk av enheter, inkludert små RFID-tagger og datamaskiner.
Forfatterne undersøker også implementeringen av post-kvante homomorf kryptering og offentlig nøkkelkryptografi.
#3. Lattices and Their Application in Cryptography
Dette er ikke en bok, men en avhandling skrevet av Merve Cakir i 2014. Målet er å identifisere egenskapene til gitterbaserte kryptosystemer og hvordan bruken av signatur- og krypteringssystemer blir usikker i møte med kvantedatamaskiner.
I avhandlingen foreslår forfatteren en alternativ kryptografi basert på gitterproblemer. Utfordringer og sikkerhet ved beregningsproblemer analyseres gjennom et samarbeid mellom kompleksitetsteori, offentlig nøkkelkryptografi og lineær algebra.
#4. Basic to Advanced Level Cryptography
Dette kurset, som tilbys via Udemy, gir en klar oversikt over kryptografi og relaterte konsepter. Kurset dekker kryptografi, hashing, hacking, kryptoanalyse og krypterings-/dekrypteringsprosesser.
Det er delt inn i 5 seksjoner med 17 forelesninger, med en total varighet på 2 timer og 7 minutter. For å delta, trenger du grunnleggende datakunnskaper og matematikk fra videregående skole.
Konklusjon
Kryptografi er en enkel, men kraftig metode for å beskytte informasjon. Den benytter seg av komplekse matematiske problemer og algoritmer for å sikre data, som er et prioritert mål for mange i dagens samfunn.
Gitterbasert kryptografi er en av de sikreste mekanismene for å beskytte data. Den benytter lineær algebra til å kryptere data. Gitter, vektorer og grunnlag benyttes for å konstruere komplekse mønstre. Dekrypteringsmetoden er avhengig av disse mønstrene, og kun de med tilgang til opprinnelsespunkter kan dekryptere informasjonen. Hvis du har nøkkelen, er dekryptering enkelt.
Gitterbasert kryptografi er en veletablert teknikk for å sikre data for enkeltpersoner og bedrifter på tvers av flere bransjer, fra IT og sikkerhet til finans og mange andre.
Du kan også lese om skykryptering (Cloud Cryptography).