Viktigheten av sortering i databehandling
Sortering av lister med data er en fundamental prosess i mange applikasjoner. Det er et sentralt element for å presentere informasjon på en oversiktlig måte og for å utføre effektive søk. Derfor er det essensielt for en dyktig programvareutvikler å ha god forståelse for hvordan man sorterer datasamlinger. Denne artikkelen vil ta for seg noen av de mest brukte algoritmene for sortering av arrayer i JavaScript.
Hva er sortering og hvorfor er det viktig?

Kilde: Unsplash
Sortering handler om å systematisk ordne verdier etter et bestemt kriterium. Denne rekkefølgen kan være enten stigende eller synkende. Sortering av arrayer i JavaScript er en viktig ferdighet, fordi det gjør data mer leselig og lettere å forstå.
Et eksempel er sortering av filer etter dato, der de nyeste filene vises først, eller produkter som er sortert etter pris. Det er også et viktig skritt for å kunne bruke binære søk, som krever sortert data for å fungere.
Selv om det finnes innebygde funksjoner og biblioteker for sortering, er det viktig å forstå algoritmene som ligger under for å prestere godt i jobbintervjuer og for å kunne skrive kode på lavt nivå.
Sorteringsalgoritmer for JavaScript Arrayer
Boblesortering

Boblesortering er ansett som en av de enkleste algoritmene å forstå og implementere. Den fungerer ved å iterere gjennom arrayet flere ganger. I hver iterasjon sammenlignes to etterfølgende elementer, og de byttes om hvis de er i feil rekkefølge.
Vi kjører gjennom arrayet n ganger, der n er antall elementer. For hver gjennomgang flyttes de største elementene mot slutten av arrayet. Følgende pseudokode viser hvordan man sorterer tall i stigende rekkefølge:
1. La n være antall elementer i arrayet
2. Gjenta n ganger, bruk i for å holde telling på løkkene
a. Gjenta gjennom arrayet fra andre element til (n - i)-te element
b. Hvis forrige element er større enn gjeldende element, bytt dem om.
Overført til JavaScript, vil koden se slik ut:
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
}
}
return arr;
}
For å bedre visualisere hva som skjer, anbefales det å legge til console.log-setninger inne i de to løkkene. Dette vil vise hvordan arrayet endrer seg i hver gjennomgang.
I koden nedenfor er sorteringsfunksjonen modifisert med `console.log` i hver løkke. Et lite, usortert array sorteres også med denne funksjonen.
function sort(arr) {
const n = arr.length;
for (let i = 0; i < n; i++) {
console.log(`Pass: ${i}`);
for (let j = 1; j < n - i; j++) {
if (arr[j - 1] > arr[j]) {
const temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
console.log(arr);
}
}
return arr;
}
const array = [9, 2, 7, 4, 1];
sort(array);
console.log(array);
Resultatet av å kjøre denne koden vil være:

Boblesortering har en tidskompleksitet på O(n^2). Dette skyldes at den utfører n gjennomganger, som går gjennom arrayet for hver gang. Det betyr at den ikke skalerer godt. På den andre siden har den en romkompleksitet på O(1), da den modifiserer array-elementene på stedet.
Innsettingssortering

Innsettingssortering er en annen populær sorteringsalgoritme for JavaScript-arrayer. For å sortere i stigende rekkefølge, plukker vi et tall (som vi kaller «num»), og flytter det mot venstre så lenge det er større enn de andre tallene til venstre for det. Dette gjøres for hvert tall i arrayet fra det andre elementet og utover. Her er en beskrivelse i pseudokode:
1. La n være antall elementer i arrayet
2. Gå gjennom arrayet fra element 1 til n-1 (start fra det andre elementet)
a. Sett currentElement til array[i]
b. Sett j til i - 1
c. Så lenge j >= 0 og array[j] > current_element
i. Flytt array[j] til array[j+1]
ii. Reduser j med 1
d. Sett array[j+1] til current_element
Implementert i JavaScript ser det slik ut:
function insertionSort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
}
return array;
}
Som med boblesortering, vil console.log-setninger hjelpe deg å se prosessen. Kodesnutten nedenfor viser hvordan innsettingssortering fungerer:
function sort(array) {
const n = array.length;
for (let i = 1; i < n; i++) {
const currentElement = array[i];
let j = i - 1;
console.log("Placing element:", currentElement);
while (j >= 0 && array[j] > currentElement) {
array[j + 1] = array[j];
j -= 1;
}
array[j + 1] = currentElement;
console.log("Placed it at position:", j + 1);
console.log(array);
}
return array;
}
const array = [4, 1, 2, 5, 3];
sort(array);
Kjøring av denne koden vil produsere følgende resultat:
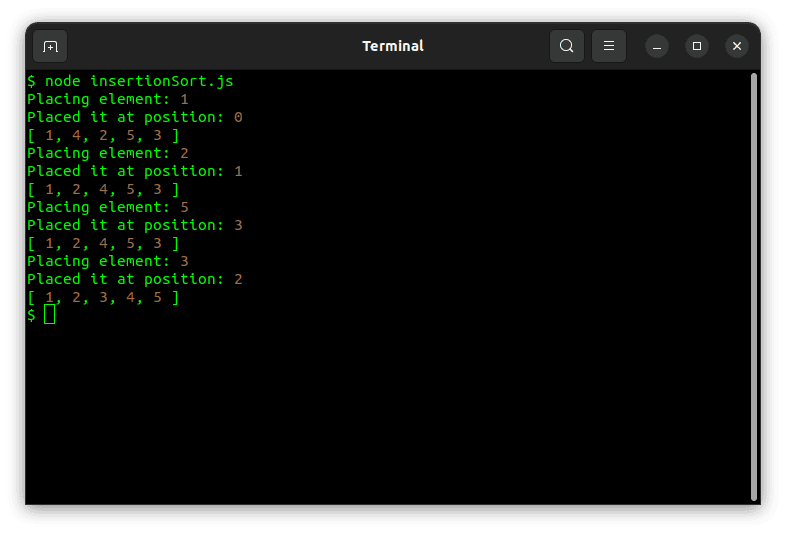
Flettesortering

Mens innsettings- og boblesortering har kvadratisk tidskompleksitet, har flettesortering kvasi-lineær tidskompleksitet, O(n * log(n)).
Flettesortering bruker en «del og hersk» strategi. Arrayet deles gjentatte ganger opp i mindre deler, helt til det bare er enkelt elementer igjen. Deretter flettes de sammen igjen.
Oppdelingen er rekursiv, slik at del-arrayene settes sammen tilbake etterpå.
Når de slås sammen igjen, gjøres det i sortert rekkefølge. Selve sammenslåingen er det samme som å slå sammen to allerede sorterte arrayer. Pseudokoden for dette er som følger:
1. Hvis lengden på arrayet er 1 eller mindre, returner arrayet (base case)
2. Finn midtpunktet
a. Sett mid til avrundet (lengden på arrayet / 2)
3. Del arrayet i to delarrayer
a. Lag leftArray og kopier første halvdel av arrayet inn i det (fra 0 til mid)
b. Lag rightArray og kopier andre halvdel av arrayet inn i det (fra mid+1 til slutten)
4. Kall MergeSort rekursivt på leftArray
5. Kall MergeSort rekursivt på rightArray
6. Slå sammen de to sorterte delarrayene:
a. Lag en tom resultArray
b. Så lenge både leftArray og rightArray ikke er tomme
i. Hvis første element i leftArray er mindre eller lik første element i rightArray, legg det til i resultArray
ii. Ellers, legg første element i rightArray til i resultArray
c. Legg til eventuelle gjenværende elementer i leftArray i resultArray (hvis det finnes noen)
d. Legg til eventuelle gjenværende elementer i rightArray i resultArray (hvis det finnes noen)
7. Returner resultArray
Implementert i JavaScript vil det bli:
function sort(array) {
// Base case in which we stop subdividing the array
if (array.length == 1) {
return array;
}
// Finding the middle point of the array
const m = Math.round(array.length / 2);
// Divide the array into two halves
const leftUnsorted = array.slice(0, m);
const rightUnsorted = array.slice(m);
// Recursively call merge sort
const leftSorted = sort(leftUnsorted);
const rightSorted = sort(rightUnsorted);
// Return a merged sorted array
return merge(leftSorted, rightSorted);
}
function merge(left, right) {
// Merge two sorted lists
let result = [];
let leftIndex = 0;
let rightIndex = 0;
while (leftIndex < left.length && rightIndex < right.length) {
if (left[leftIndex] < right[rightIndex]) {
result.push(left[leftIndex]);
leftIndex += 1;
} else {
result.push(right[rightIndex]);
rightIndex += 1;
}
}
return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}
Hvis du kjører koden med et eksempelarray, skal den fungere:
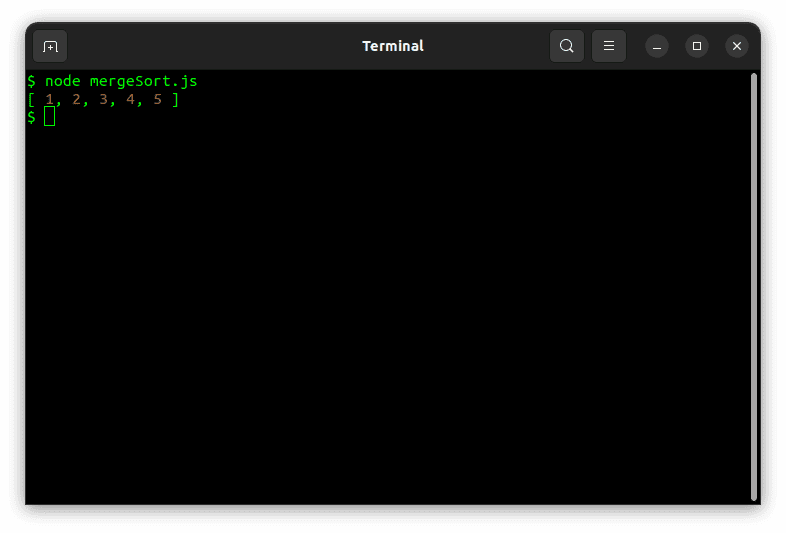
Quicksort

I likhet med flettesortering, bruker quicksort «del og hersk»-strategien. Algoritmen velger et «pivot»-element, og flytter deretter alle elementer som er større enn pivoten til høyre, og alle som er mindre til venstre. Når dette er gjort, vil pivot-elementet være i riktig posisjon.
For å flytte elementer rundt pivoten, starter vi med å flytte pivoten til slutten av arrayet.
Deretter bruker vi en peker fra venstre side av arrayet, og ser etter det første tallet som er større enn pivoten. Samtidig bruker vi en annen peker fra høyre side, og ser etter det første tallet som er mindre enn pivoten. Når begge disse tallene er funnet, bytter vi dem. Denne prosedyren fortsetter til pekeren fra venstre er større enn den fra høyre.
Når prosedyren stopper, bytter vi det største av de to sist byttede tallene med pivot-elementet. Da er pivot-elementet på riktig plass, med alle tall mindre enn det til venstre, og alle større tall til høyre.
Denne prosedyren gjentas rekursivt for delarrayene på venstre og høyre side av pivoten, helt til delarrayene bare har ett element hver.
Her er pseudokoden for quicksort:
1. Hvis lessThanPointer er mindre enn greaterThanPointer:
a. Velg en pivot fra arrayet
b. Flytt elementer slik at mindre elementer kommer til venstre, og større elementer kommer til høyre
c. Kall Quicksort rekursivt på leftSubarray
d. Kall Quicksort rekursivt på rightSubarray
Og overført til JavaScript:
function sort(array, low, high) {
if (low < high) {
// Choose the pivot index and partition the array
const pivotIndex = move(array, low, high);
// Recursively sort the subarrays to the left and right of the pivot
sort(array, low, pivotIndex - 1);
sort(array, pivotIndex + 1, high);
}
}
function move(array, low, high) {
// Select the pivot element (in this case, the last element)
const pivotElement = array[high];
// Initialize the index for the smaller element
let i = low - 1;
for (let j = low; j < high; j++) {
// If the current element is less than or equal to the pivot, swap it with the element at index i+1
if (array[j] <= pivotElement) {
i += 1;
const temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
// Swap the pivot element into its correct position
const temp = array[i];
array[i] = array[j];
array[j] = temp;
// Return the index of the pivot element
return i + 1;
}
Sortering av et eksempelarray med quicksort i Node.js vil gi følgende:
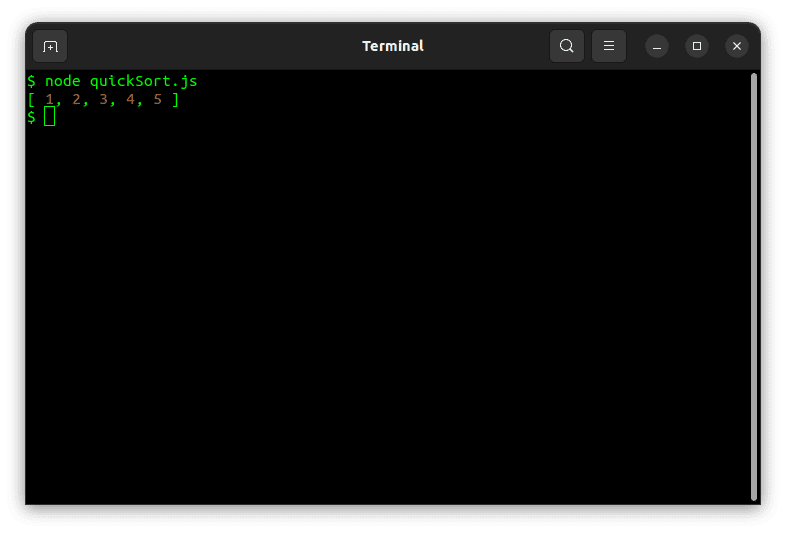
I beste fall har quicksort en kvasi-lineær tidskompleksitet. Plassbruken i quicksort er også logaritmisk, noe som gjør det til en relativt effektiv sorteringsalgoritme.
Tips for kodeintervju
❇️ Øvelse er nøkkelen. Det hjelper deg med å lære algoritmene, og ikke minst utvikle problemløsnings- og analytiske ferdigheter. Du kan øve på plattformer som Leetcode og AlgoExpert.
❇️ Prøv å løse problemet selv først. Istedenfor å se på løsningen umiddelbart, prøv å løse den selv. Det vil hjelpe deg å utvikle problemløsningsferdighetene dine.
❇️ Hvis et problem tar for lang tid, kan du se på løsningen, og lære av den. De fleste plattformer for læring tilbyr løsninger. ChatGPT eller Google Bard kan også hjelpe deg med å forstå konseptene.
❇️ Ikke begynn å kode med en gang. Planlegg løsningene dine og tenk gjennom dem før du begynner å kode. Pseudokode er en god måte å notere ideer på.
Konklusjon
I denne artikkelen har vi sett på de mest brukte sorteringsalgoritmene. Det kan virke overveldende å lære dette i starten, men vi anbefaler å bruke flere forskjellige kilder, istedenfor å stole på bare én. Lykke til med kodingen!
Du kan også lese mer om den sorterte funksjonen i Python.